1 Dense & MOE

Dense：每次激活全部参数。

MoE ：用一个轻量级的路由器，为每个输入的 Token，动态地、稀疏地选择一小部分专家来激活和计算。专家通常就是FFN。

1

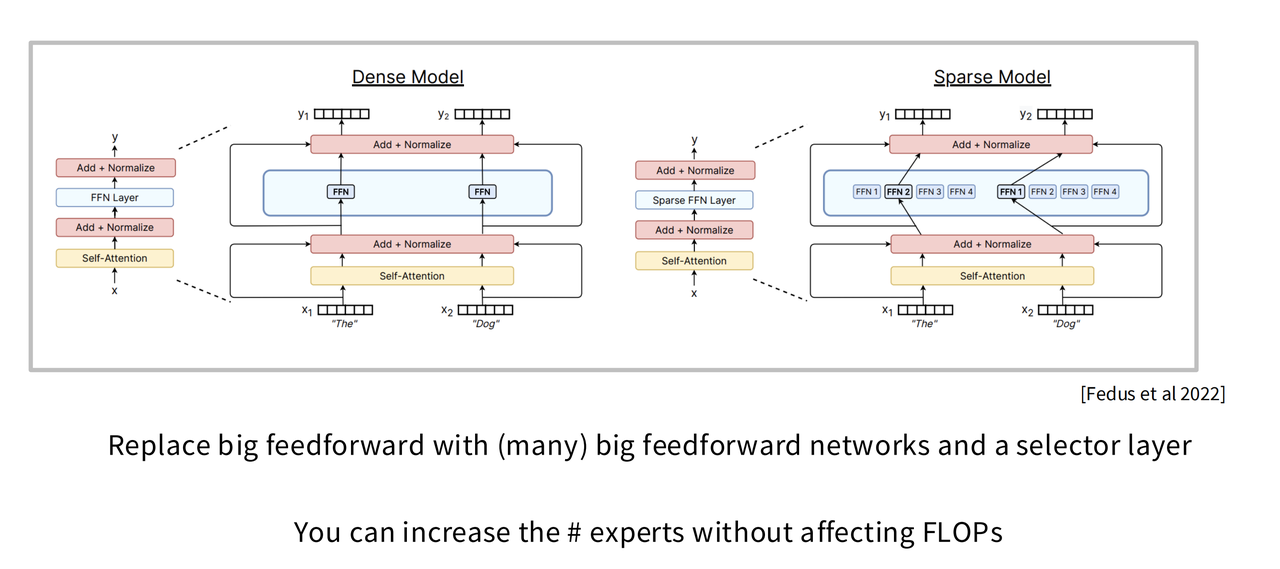
这样做的好处是什么？假设我们有64个专家，但路由器每次只选择2个。那么：

  1. 参数量巨大：模型的总参数量是64个专家的总和，规模非常庞大，这让它有能力“记忆”更多的世界知识。
  2. 计算量不变：在一次前向传播中，每个 Token 实际只经过了2个专家的计算。如果每个专家的大小和原始密集模型的FFN大小相仿，那么计算成本（FLOPs）就只增加了路由器的开销，几乎可以忽略不计。

一句话总结：MoE 用“总参数量巨大”换取了“知识容量”，同时通过“稀疏激活”维持了极低的“计算成本”。

2 路由器如何选择专家？

2

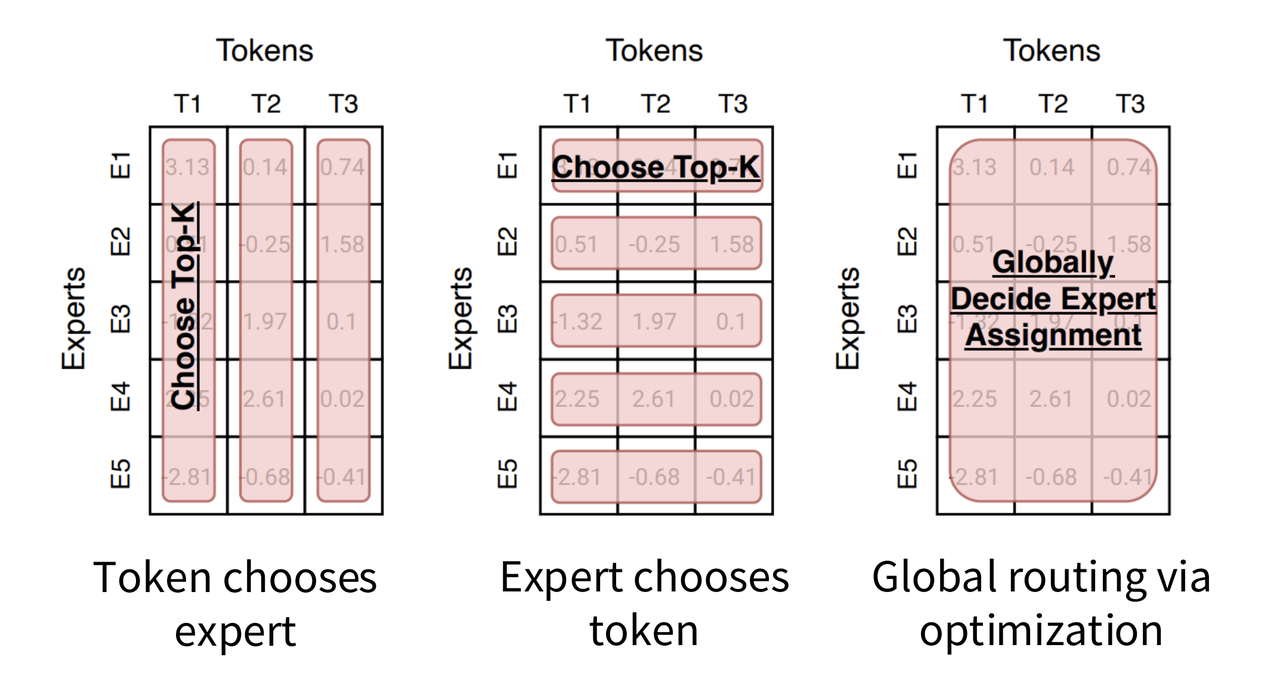
可以想到有很多种选择方式，但越复杂的规则训练越麻烦，因此目前主流是token选择k个专家。

3 主流top k routing方法

token采用什么方式选择k个专家？比如RL选，运筹学解，但是都太复杂，还是训练复杂的问题。

这里介绍主流top k routing方法。

3

4

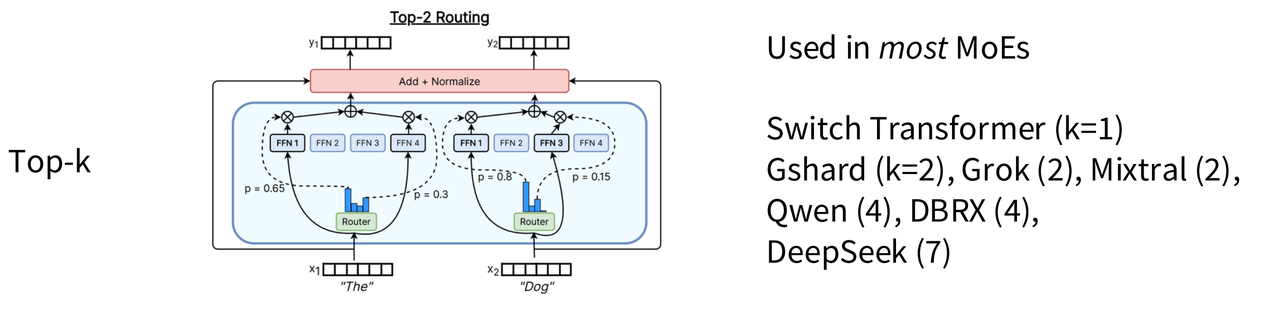
我们以处理单个 Token t 的第 l 层 MoE 模块为例，并假设 K=2。

第 1 步：输入就位 (Input)

一个 Token 经过前序模块的计算，以向量 $u_t^l$ 的形式抵达 MoE 层。这个向量是该 Token 在当前层的丰富语义表示。

第 2 步：计算“亲和度”并归一化 (Affinity Scoring & Normalization)

路由器需要判断该将这个 Token $u_t^l$ 发送给哪个专家。为此，它为每个专家 i 维护一个可学习的“身份”向量 $e_i^l$。

路由器通过计算输入向量 $u_t^l$ 与每一个专家身份向量 $e_i^l$ 的点积 (dot product)，来衡量它们之间的“亲和度”或“匹配度”。点积结果越大，代表该专家越适合处理这个 Token。

随后，应用 Softmax 函数。

$$s_{i,t} = Softmax_i (u_t^{l^T} * e_i^l)$$
  • $(u_t^{l^T} * e_i^l)$ 就是计算亲和度的点积操作。
  • $Softmax_i$ 对所有 N 个专家的亲和度分数进行归一化，得到一组总和为 1 的权重 $s_{i,t}$。

第 3 步：选出 Top-K 专家 (Top-K Selection)

路由器查看所有专家的 Softmax 权重 $s_{j,t}$，并从中选出得分最高的 K 个（这里是2个）。

$$Topk({s_{j,t} | 1 <= j <= N}, K)$$

第 4 步：生成稀疏门控 (Gating)

这是实现“稀疏激活”的关键一步。路由器会生成一个“门控”值 $g_{i,t}$。

  • 如果专家 i 是被选中的 Top-K 专家之一，那么它的门控值 $g_{i,t}$ 就等于它在上一步计算出的 Softmax 权重 $s_{i,t}$。
  • 如果专家 i 未被选中，它的门控值 $g_{i,t}$ 则被强制设为 0。

这样，我们就得到了一个稀疏的门控向量，其中只有 K 个位置有非零值。

$$g_{i,t} = \begin{cases} s_{i,t}, & s_{i,t} \in \text{Topk}(\{s_{j,t} | 1 \le j \le N\}, K), \\ 0, & \text{otherwise,} \end{cases}$$

第 5 步：并行计算与加权汇总 (Gated Aggregation)

输入向量 $u_t^l$ 被同时发送给所有 N 个专家（在概念上）。每个专家 i 都对其进行一次前馈网络计算 $FFN_i(u_t^l)$。

但是，由于门控值 $g_{i,t}$ 的作用，只有被选中的 Top-K 个专家的计算结果会被保留，其余 N-K 个专家的输出都会因为乘以 0 而被丢弃。

最后，将所有专家的输出与其对应的门控值相乘，再求和，得到 MoE 层的核心输出。这个过程本质上是一个加权平均，权重就是稀疏的门控值。

$$Σ (g_{i,t} * FFN_i(u_t^l))$$

第 6 步：残差连接 (Residual Connection)

与标准 Transformer 模块一样，为了保证信息流的通畅和训练的稳定性，我们将 MoE 层的计算结果与原始输入 $u_t^l$ 相加。

$$\mathbf{h}_{t}^{l} = \sum_{i=1}^{N} \left( g_{i,t} \text{FFN}_{i} \left( \mathbf{u}_{t}^{l} \right) \right) + \mathbf{u}_{t}^{l},$$

4 MOE变体

早期的 MoE 想法很直接：把一个标准的 FFN 复制 N 份，就成了 N 个专家。但很快，研究者们发现了一些更聪明的玩法，尤其是以 DeepSeek 等模型为代表的创新，让 MoE 的效率更上一层楼。

5

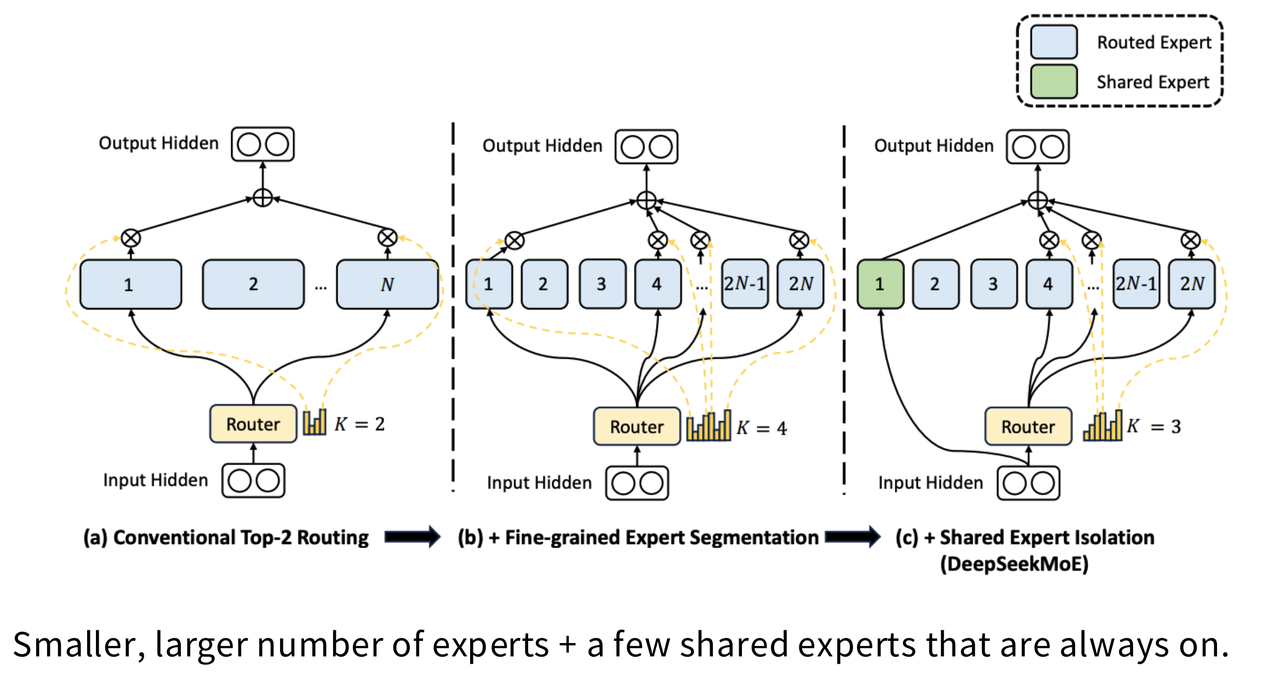
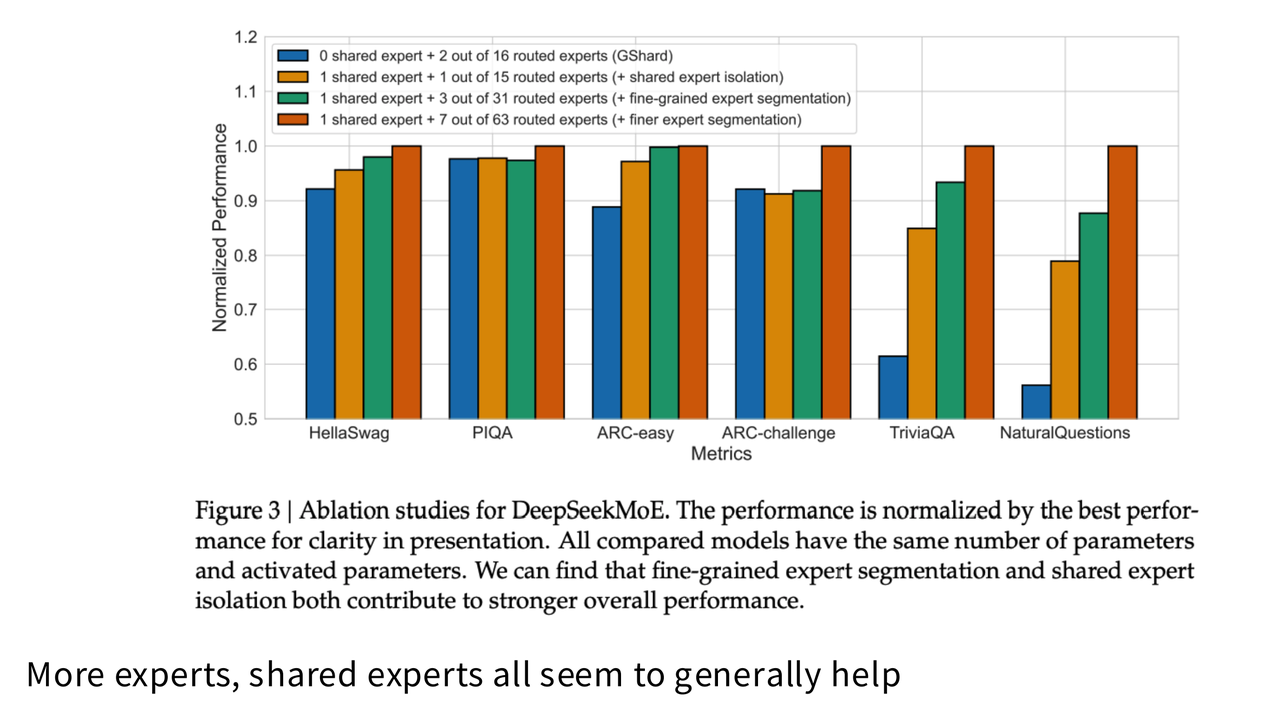
  • 思想：为什么要让每个专家都那么“胖”呢？我们可以把每个专家的规模（例如，中间层的维度）缩小，比如缩小到原来的1/4。这样一来，在总参数量不变的前提下，我们就可以拥有4倍数量的专家！
  • 好处：专家数量越多，模型的分工可以更细致，路由器的选择也更丰富、更灵活。实践证明，在计算量相当的情况下，拥有大量细粒度的专家，其性能通常优于少量“臃肿”的专家。
  • 思想：会不会有一些基础的、通用的计算模式，是所有 Token 都需要处理的？如果每次都通过路由器去选择专家来执行这些通用任务，似乎有点浪费。
  • 方案：因此，研究者们提出，除了那些需要被路由选择的“路由专家”外，再设立一两个“共享专家”。每个 Token 在被送往路由专家的同时，也必须经过这些共享专家的处理。
  • 效果：这种“公私结合”的模式，让模型既能处理通用模式，又能进行个性化、专业化的处理。DeepSeek 的一系列实验表明，这种设计能带来显著的性能提升。

6

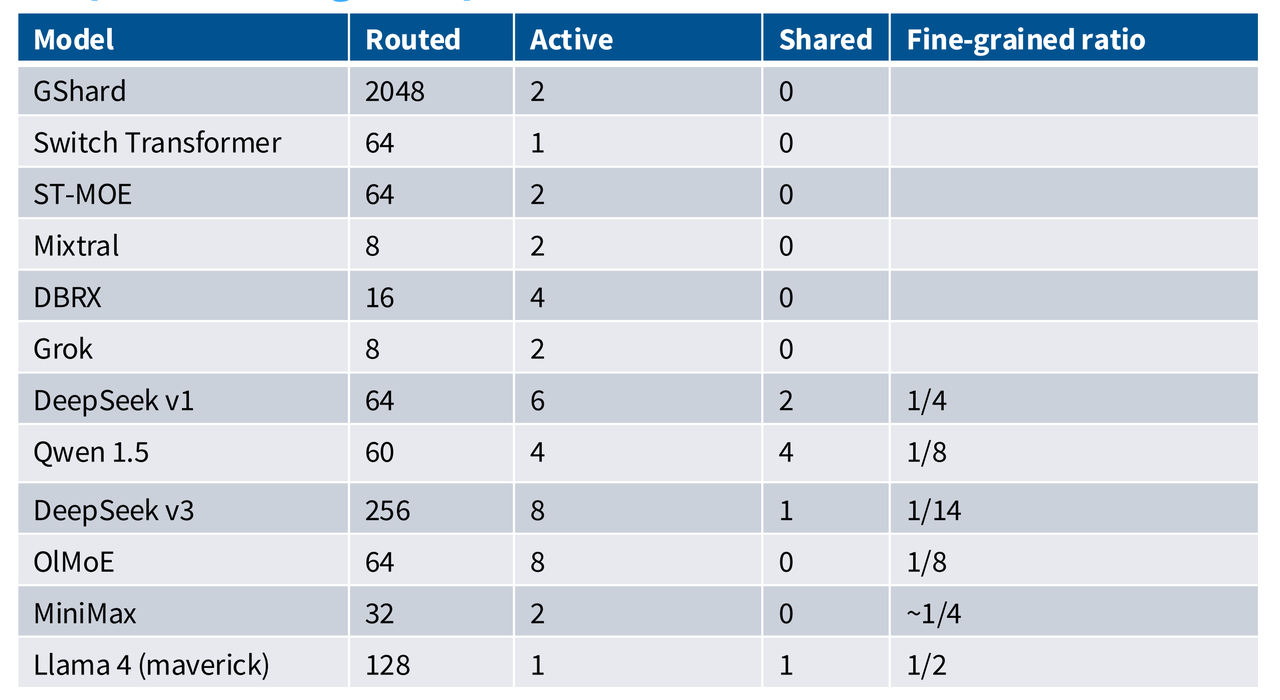
主流大模型的MOE参数：

7

5 训练MOE

MoE最大的一个难题在于：路由决策是离散的（选或不选），而深度学习的基石——梯度下降——最喜欢的是平滑、可微的函数。 这个矛盾导致了训练上的两个核心痛点：

  1. 梯度回传困难：路由器做出“选择”这个动作，本身是不可微分的。我们无法直接通过梯度告诉路由器：“嘿，你上次选错了专家，下次应该选另一个！” 训练信号的传递非常间接和微弱。
  2. 负载不均衡 (Load Imbalance)：由于某些专家可能天然更“受欢迎”，在训练初期，路由器可能很快就学会了只把大量的 Token 送给少数几个专家，导致“强者愈强，弱者愈弱”。这会让大部分专家参数得不到有效训练，模型容量被严重浪费，就像一个团队里只有几个人在拼命干活，其他人都在“摸鱼”。

为了解决这些问题，研究者们设计了一种巧妙的“辅助损失函数”（Auxiliary Loss）。在计算模型主要的预测损失（比如预测下一个词的准确率）之外，还会额外计算一个“负载均衡损失”。

5.1 Deepseek v1/v2

8

这个损失函数的设计目标是：惩罚那些导致专家负载不均衡的路由行为。 它会统计每个专家在一批数据中被分配了多少 Token，如果发现分配得非常不均匀，就会产生一个较大的损失值。这个损失值会被加到总损失中，通过梯度下降，间接地“劝告”路由器：“下次分配得均匀一点，不然就罚你！”

图中的公式来自 DeepSeek 团队的技术分享，展示了 MoE 模型中至关重要的“平衡损失函数”（Balancing Loss），

Per-Expert Balancing（专家粒度的平衡）

这是 MoE 中最核心的平衡策略，旨在确保所有专家都能获得大致相等的训练机会。如果某些专家很少被选中，它们将得不到充分训练；反之，如果少数专家承担了绝大部分工作，它们就会成为性能瓶颈，也违背了 MoE 专业分工的初衷。

图中的公式 (12), (13), (14) 定义了专家平衡损失：

$$P_i = (1/T) * Σ s_i,t$$

含义: $P_i$ 计算了在整个批次（Batch）的 T 个 token 中，路由器分配给第 i 个专家的平均路由概率。 $s_i,t$ 是路由器对于 token t 分配给专家 i 的概率值。

目的: 这个值反映了路由器“倾向于”选择专家 i 的平均置信度。

$$f_i = (N' / K'T) * Σ 1(Token \ t \ selects \ Expert \ i)$$

含义: $f_i$ 计算了被实际路由到第 i 个专家的 token 比例。Σ 1(...) 是一个计数器，统计了批次中有多少 token 最终选择了专家 i。N' 是专家总数，T 是 token 总数。（这里的 K' 是指 Top-K 的 K 值）。

目的: 这个值直接衡量了专家 i 的实际“工作量”或负载。

$$ℒ_{ExpBal} = α_1 * Σ(f_i * P_i)$$

含义: 这是最终的专家平衡损失函数。它通过将每个专家的负载比例 $f_i$ 和其平均路由概率 $P_i$ 相乘，然后求和得到。 $α_1$是一个超参数，用来调节这个辅助损失在总损失中的权重。

工作原理: 这个损失函数同时惩罚了两种不均衡的情况：1) 某个专家的 $f_i$ 过高（负载过重）；2) 某个专家的 $P_i$ 过高（路由器过度自信地倾向于它）。为了最小化这个损失，模型必须学会将 token 均匀地分配给所有专家，即让所有专家的 $f_i$ 和 $P_i$ 都趋于一个较小且接近的值。

Per-Device Balancing（设备粒度的平衡）

当模型规模非常大，需要将专家分布到多个计算设备（如 GPU）上进行训练时（即专家并行，Expert Parallelism），仅仅保证专家间的负载均衡是不够的。我们还需要确保每个设备上的计算负载是均衡的，否则，负载较重的设备会成为整个训练流程的瓶颈，导致其他设备空闲等待，降低硬件利用率。

图中的公式 (15), (16), (17) 正是为了解决这个问题：

$$f'_i = (1 / |ℰ_i|) * Σ f_j$$

含义: 计算了第 i 个设备上所有专家的平均 token 比例。 $ℰ_i$ 是部署在设备 i 上的专家集合， $f_j$ 是该设备上某个专家的负载。

目的: 衡量了设备 i 的平均计算负载。

$$P'_i = Σ P_j$$
  • 含义: 计算了路由器分配给第 i 个设备上所有专家的总路由概率。
  • 目的: 衡量了路由器将计算任务分配到设备 i 的总倾向。
$$ℒ_{DevBal} = α_2 * Σ(f'_i * P'_i)$$

含义: 这是设备平衡损失，其结构与专家平衡损失类似，但聚合的层级是设备。 $α_2$ 是对应的超参数。

工作原理: 通过最小化这个损失，可以促使路由器不仅在专家间进行均衡分配，还要考虑到这些专家所在的物理设备，从而实现跨设备的计算负载均衡。

5.2 deepseek v3

10

Auxiliary Loss Free Balancing

免辅助损失的平衡策略**，**其核心思想是引入“每个专家的偏置（per-expert biases）”。

  1. 通过可学习的偏置（Bias）直接干预路由

传统的 MoE 模型完全依赖于一个辅助损失函数来“间接”地引导路由器学会均衡地分配 token。

DeepSeek v3 提出了一种更直接的方法：

  • 为每个专家设置一个可学习的偏置项 $b_i$。
  • 在选择专家时，不再仅仅比较路由器为每个专家生成的原始分数 $s_{i,t}$，而是比较“分数 + 偏置”，即 $s_{i,t} + b_i$。
$$ g'_{i,t} = \begin{cases} s_{i,t}, & s_{i,t} + b_i \in \text{Topk}(\{s_{j,t} + b_j | 1 \le j \le N_r\}, K_r), \\ 0, & \text{otherwise.} \end{cases}$$

对于一个 token t，路由决策（即选择哪些专家）是基于 $s_{j,t} + b_j$ 这个新分数来决定的。只有那些新分数排进前 $K_r$ 名的专家才会被选中。

  • $b_i$ 的作用就像一个“优先权调节器”。如果某个专家 i 在一段时间内接收的 token 太少，系统可以通过提高它的 $b_i$ 值，使其在下一次路由竞争中更有优势，从而“吸引”更多的 token。反之，如果某个专家负载过重，就可以降低其 $b_i$ 值。
  • 这种对 $b_i$ 的调整是在线学习（online learning）的，意味着它可以在训练过程中被动态、快速地更新，以实时响应负载的变化。
  • 请注意：偏置 $b_i$ 只影响专家选择的过程。一旦专家 i 被选中，最终的门控值（gating value）仍然是原始分数 $s_{i,t}$，而不是 $s_{i,t} + b_i$。这确保了偏置项不会影响专家输出的加权求和。
  1. “免辅助损失”的真相：一个并非完全“免”的策略

尽管该方法被称为“免辅助损失”，但是它并非完全没有辅助损失。

  • DeepSeek-V3 主要依赖这种免损失的策略，但为了防止在单个序列内出现极端的不平衡，它还会额外使用一个“补充性的序列级平衡损失（complementary sequence-wise balance loss）”。
  • 这意味着：基于偏置的在线调整是主要的、主动的平衡手段，而辅助损失则像一个“安全网”，用于处理一些极端情况，确保系统不会失控。

总而言之，DeepSeek v3 的这项技术通过引入可在线学习的“专家偏置”，实现了一种更主动、更直接的负载均衡控制，同时保留了传统的辅助损失作为补充，以应对极端情况。这代表了对 MoE 训练稳定性和效率的进一步优化探索。

5.3 MoE 训练的核心注意事项

  1. 平衡损失权重 α：α1 和 α2 的选择至关重要。如果太小，将无法有效约束路由器的行为，导致负载不均；如果太大，则可能干扰主任务的学习。这通常需要通过实验进行调试。
  2. 专家容量（Expert Capacity）：为了在硬件上实现高效计算，通常会为每个专家设置一个“容量”，即它在一个批次中最多能处理的 token 数量。如果路由到某个专家的 token 数量超过其容量，多余的 token 会被“丢弃”（dropped），即它们不会经过这个 MoE 层的专家网络计算。设置合适的容量因子（Capacity Factor）对于平衡计算效率和模型性能非常重要。
  3. 路由策略和稳定性：除了平衡损失，还可以采用一些技巧来提升路由的稳定性，例如在路由器的 logits 上增加噪声，以鼓励在训练初期进行更多的探索，避免路由器过早地“锁定”少数几个专家。
  4. 分布式训练方案：对于大规模 MoE 模型，必须采用专家并行、数据并行等混合并行策略。Per-device balancing 的思想在这种情况下尤为关键，它直接关系到分布式训练的整体效率。