《Sample More to Think Less: Group Filtered Policy Optimization for Concise Reasoning》
解决大语言模型在通过强化学习(RL)提升准确率时,普遍存在的“响应长度膨胀”问题。作者指出,许多模型为了追求更高的分数,会生成大量冗长、重复的“填充”性文本,这在推理时造成了不必要的计算浪费。为解决此问题,论文提出了GFPO (Group Filtered Policy Optimization,组过滤策略优化)。其核心思想:在训练阶段“想得更多”,通过采样更大的响应组,并根据响应长度和**token效率(每token奖励)**这两个关键指标进行过滤,只在最优的样本上进行训练,从而教会模型在推理(测试)阶段“想得更少”,生成更简洁的回答。在多个STEM和编程基准测试中,长度膨胀减少了46-85%,同时保持了准确率。此外,自适应难度GFPO (Adaptive Difficulty GFPO),它能根据问题的实时难度动态分配训练资源,实现了效率与准确性的更优平衡。
用一次性的训练时间计算,换取持续的、部署时的推理时间计算节省,这为高效推理模型的开发提供了极具价值的新思路。

Group Filtered Policy Optimization
GFPO的核心思想是:与其在所有生成的响应上进行无差别训练,不如引入一个“过滤”步骤,有选择性地学习。其关键流程被拆解为:
1)扩大采样:对每个问题,从当前策略中采样一个比GRPO更大的响应组$\mathcal{G}=\{o_{1},...,o_{G}\}$。
2)度量与排序:根据一个用户指定的度量函数(如响应长度、token效率等),对组内所有$G$个响应进行评分和排序。
3)拒绝采样与筛选:只保留排序后最优的$k$个响应,形成子集$\mathcal{S}$(其中$k < G$)。这个过程通过一个二进制掩码$m \in \{0,1\}^G$来实现,被选中的响应$m_i=1$,被拒绝的$m_i=0$。
4)修正优势计算:这是最关键的一步。优势值的计算只在被选中的子集$\mathcal{S}$内部进行。其公式被定义为:$\hat{A}*{i,t}^{(m)}=\frac{R(q,o*{i})-\mu_{S}}{\sigma_{S}}m_{i}$。其中,$\mu_S$和$\sigma_S$分别是子集$\mathcal{S}$的奖励均值和标准差。对于被拒绝的响应($m_i=0$),它们的优势值被直接置为零,因此它们对策略更新的梯度贡献也为零。模型只从那些“表现出期望属性”(如简洁)的样本中学习如何获得高奖励。
GFPO变体:
token效率GFPO (Token Efficiency GFPO):它使用的过滤指标不是纯粹的长度,而是奖励与长度的比率 (reward/length)。这鼓励模型生成“性价比”高的响应,允许在获得足够高奖励的前提下产生较长的回答,从而追求简洁与效果的平衡。
自适应难度GFPO (Adaptive Difficulty GFPO):这是一个更智能的策略。它首先通过样本的平均奖励来实时估计问题的难度,然后动态地调整保留的样本数量$k$。对于简单问题,它采用更激进的过滤(更小的$k$)来强制模型简洁;对于难题,它保留更多的样本(更大的$k$)以鼓励充分探索。
将优势函数中的基线计算范围从整个样本组(G)缩小到经过筛选的子集(S),并将被拒绝样本的优势直接清零。这是一个极其简洁而强大的干预手段。它没有去设计复杂的惩罚项,而是让不符合期望的样本在梯度更新中“沉默”,从而以一种非常高效和直接的方式引导策略的优化方向。
实验分析
模型与基线方面,使用仅经过监督微调(SFT)的Phi-4-reasoning作为基础模型,并与经过标准GRPO训练的Phi-4-reasoning-plus进行对比,确保了比较的公平性。数据集方面,虽然训练集包含7.2万个数学问题,但作者特意限制模型在100个训练步内只看到6400个问题,这与基线的训练量完全一致,从而排除了数据量差异带来的影响。奖励函数的设计是加权的准确率和n-gram重复惩罚,值得注意的是,这个奖励函数本身已经包含了对长度的惩罚,但作者在引言中已论证其不足以抑制GRPO的长度膨胀,这反过来加强了GFPO方法的必要性。
本章最重要的贡献之一是定义了关键评估指标——超额长度缩减率 (Excess Length Reduction, ELR),其公式为:$ELR=\frac{L_{GRPO}-L_{GFPO}}{L_{GRPO}-L_{SFT}}$。这个指标衡量的是GFPO在多大程度上“抵消”了由GRPO训练所引入的额外长度。例如,100%的ELR意味着GFPO将响应长度完全恢复到了SFT基线的水平。这是一个比单纯比较绝对长度更具洞察力的指标,因为它精确地量化了新方法对“问题”(即长度膨胀)的解决程度。在组规模设置上,作者将GFPO的采样组规模G设置为8、16、24,但保留的组规模k始终小于等于8,以确保其接收的策略梯度信号数量与GRPO基线(G=8)相当,这是一个严谨的实验设计,旨在公平地隔离出“过滤”这一操作本身的效果。
结果分析
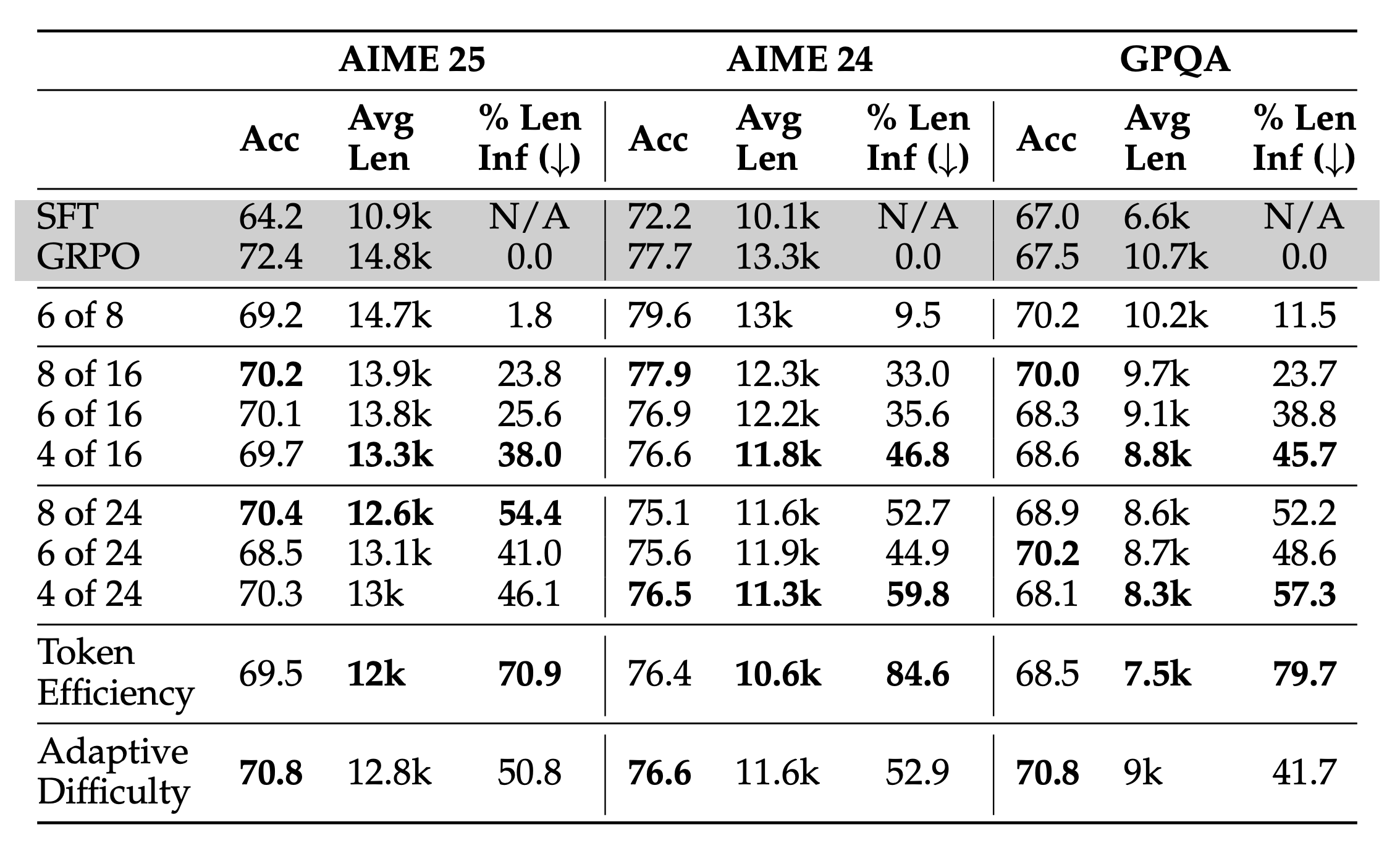
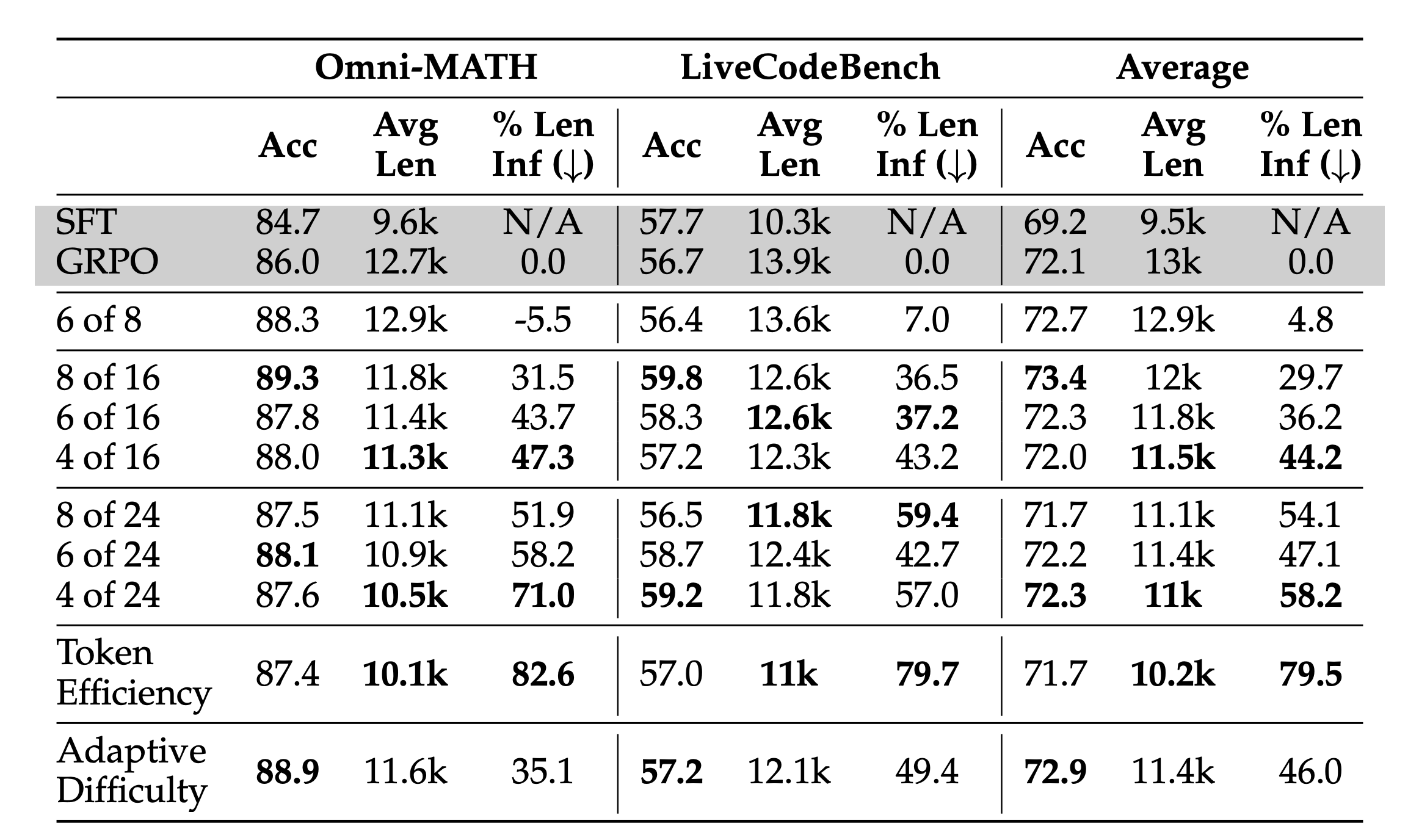
GFPO能否在保持准确率的同时,有效抑制响应长度的膨胀?其不同变体和参数(如$k$和$G$)的效果如何?作者通过在多个标准数学和代码推理基准(AIME 24/25, GPQA, Omni-MATH, LiveCodeBench)上评估三种GFPO变体(Shortest k/G, Token Efficiency, Adaptive Difficulty),得出了一系列强有力的结论。
首先,实验明确了**“想得更少,需要采得更多”**。仅在与GRPO相同的组规模内进行子采样(如Shortest 6/8),长度缩减效果微乎其微。必须扩大初始采样池(即增大$G$),才能为过滤提供足够多的优质(短)候选。其次,保留率 (k/G) 是控制长度的关键杠杆,降低保留率能有效缩短响应长度。
在所有变体中,token效率 (Token Efficiency) GFPO 表现最为亮眼,它在所有任务上都实现了最大幅度的长度缩减(高达70.9%-84.6%),同时统计上并未显著降低准确率,证明了“每token奖励”是比纯长度更优的简洁性度量。自适应难度 (Adaptive Difficulty) GFPO 则展示了其智能性,在与固定k值方法计算成本相当的情况下,它通过动态分配探索预算(即k值),在多个基准上取得了更优的长度-准确率平衡。
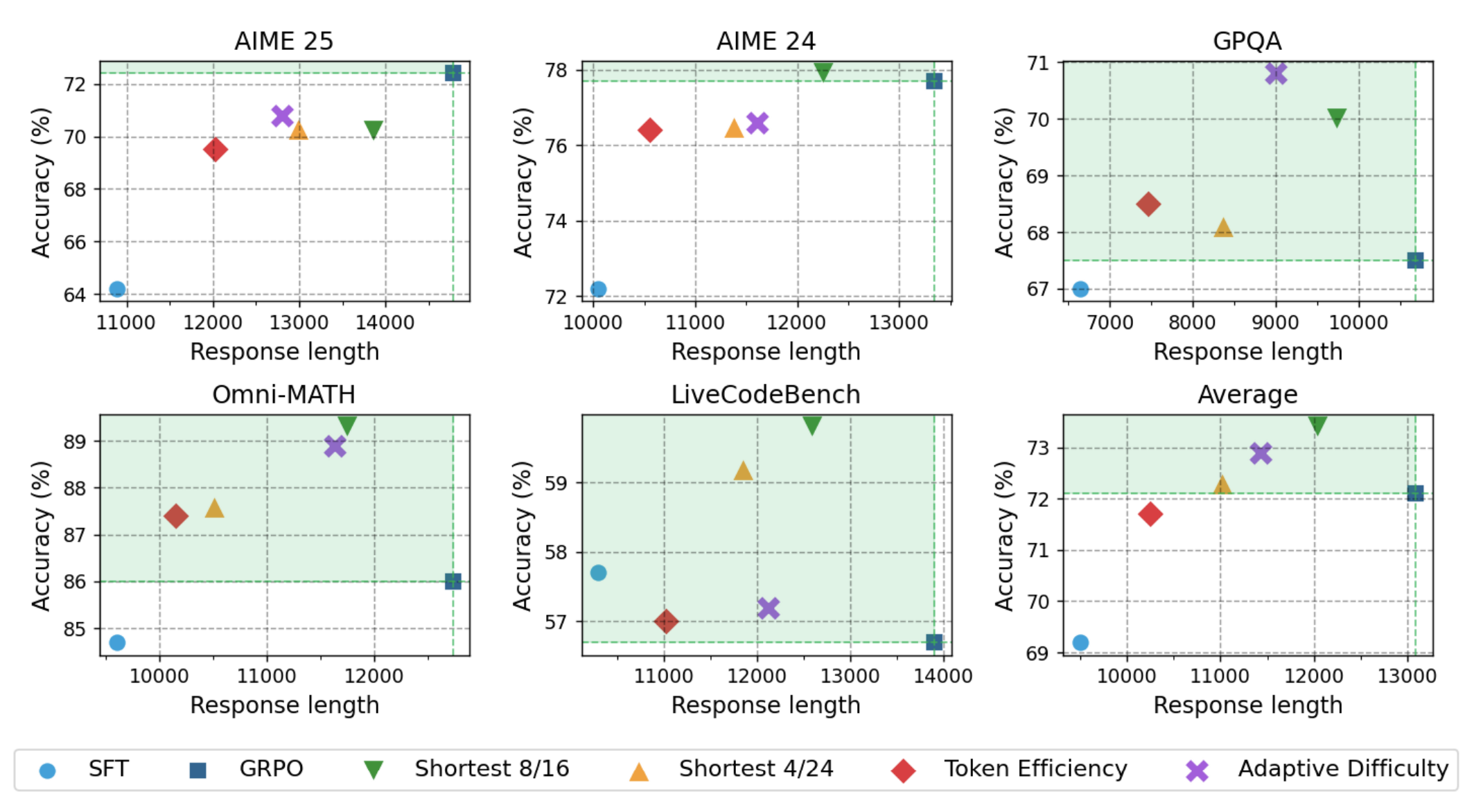
此外,GFPO在分布外(Out-of-Distribution)任务上的表现也令人印象深刻。GRPO在未见过的代码任务上同样表现出无意义的长度膨胀,而GFPO不仅抑制了这种膨胀,甚至还略微提升了准确率。本章最具启发性的部分是帕累托前沿分析 (Pareto Trade-off Analysis)。通过绘制准确率-响应长度的二维图,作者直观地展示了GFPO的多个变体在大多数基准上都严格优于GRPO——即在响应更短的同时,准确率更高。这为GFPO的有效性提供了无可辩驳的视觉证据。
分析
对GFPO的行为进行深度剖析,理解其缩减长度的具体机制,以及在不同难度问题上的表现差异。作者首先将问题按SFT模型的初始准确率划分为“简单”、“中等”、“困难”和“非常困难”四个等级。分析发现,GFPO在所有难度级别上都能有效缩短响应,其中Token Efficiency在简单问题上效果最强(甚至比SFT基线更短),而具有更大采样规模的Shortest 8/24在最难题上表现最佳。这揭示了不同策略的适用场景。
对响应内容的分段分析 (sectional analysis)。通过将模型的思考过程划分为“问题理解”、“解决方案”、“验证”和“最终答案”四个部分,作者发现GFPO削减的主要是中间冗长的**“解决方案”和“验证”**环节。它大幅减少了模型进行重复检查、兜圈子和尝试不必要分支的文本,而完整保留了对问题的复述和最终的答案。例如,在AIME 25任务上,Shortest 8/24 GFPO削减了94.4%的解决方案超额长度和66.7%的验证超额长度。
另一个关键论证是,作者通过控制问题难度,发现即使在相同难度下,更长的响应也倾向于更不准确。GRPO的许多长响应错误并非因为问题难,而是因为其固有的冗余。而GFPO通过训练模型用更短的路径解决难题,显著改善了这一点。例如,在长度小于5ktoken的响应中,GFPO解决的问题难度是GRPO的9倍。这些深入的分析不仅解释了GFPO的工作原理,更从本质上揭示了其能够培养模型形成一种更高效、更直接的推理风格。
