《The Illusion of Thinking: Understanding the Strengths and Limitations of Reasoning Models via the Lens of Problem Complexity》
这篇论文的核心启发在于,它没有停留在简单地评估大型推理模型(LRMs)在基准测试上的最终答案准确率,而是设计了一种系统性的方法来深入探究这些模型“思考”过程的内在机制和真实能力。研究发现,即使是最前沿的推理模型,在问题复杂度超过某个临界点后,其准确率会完全崩溃。一个反直觉的发现是,模型的“思考努力”(即生成的思考过程的长度)并不会随着问题变难而无限增加,反而在接近崩溃点时开始下降。通过与标准大语言模型(LLM)在同等计算资源下进行对比,研究揭示了三种性能表现区间:在低复杂度任务上,标准模型反而表现更优;在中等复杂度任务上,推理模型的“思考”显示出优势;而在高复杂度任务上,两者都会彻底失败。这套研究方法不仅揭示了模型在精确计算和逻辑一致性上的局限,也为我们理解和改进未来的推理模型指明了方向。
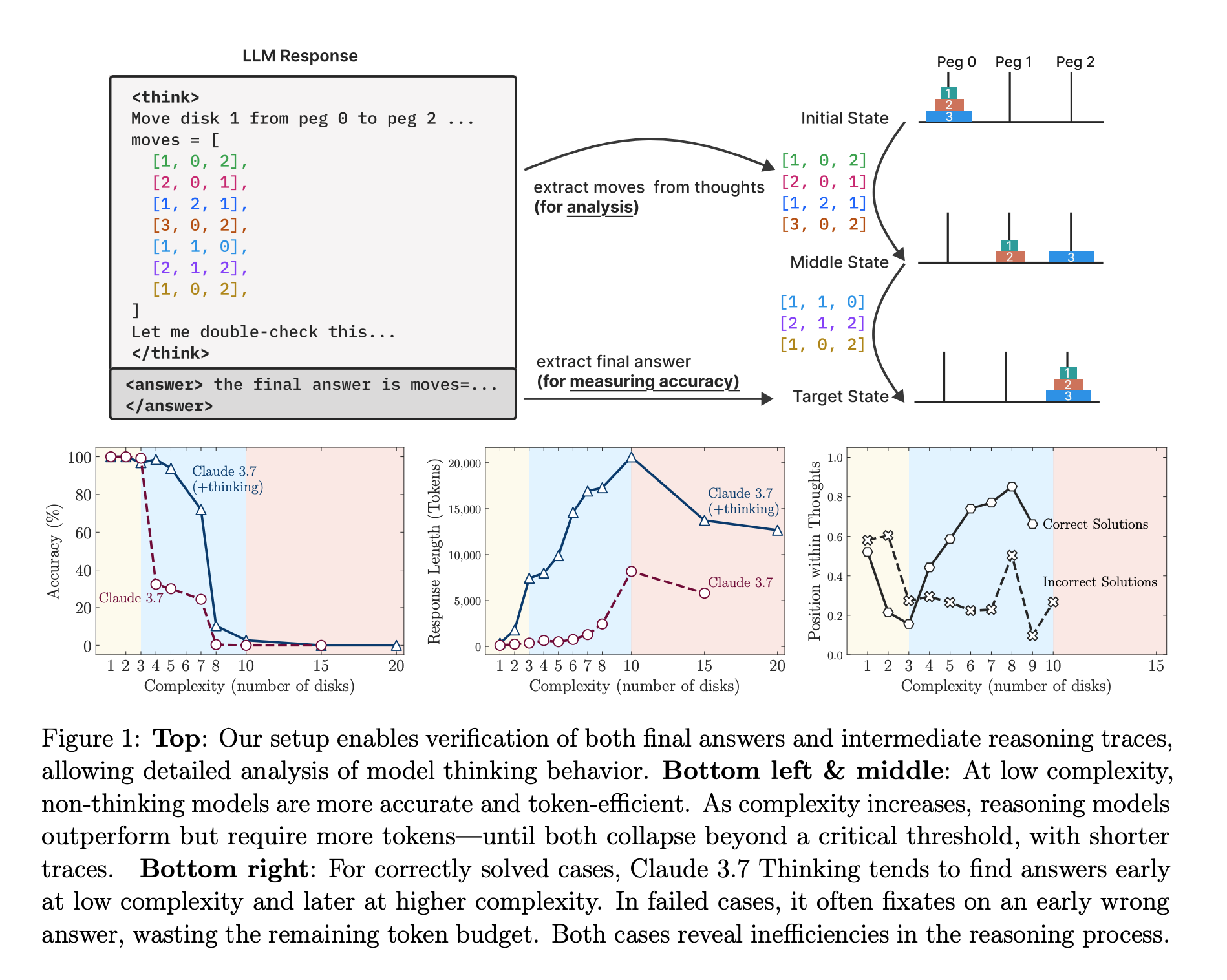
作者观察到,当前对大型推理模型(如具备“思考”功能的模型)的评估过于依赖已有的数学或代码基准,这种方式存在数据污染的风险,并且无法深入分析模型推理过程的质量和结构。为此,他们提出的关键一步是转向使用“可控的谜题环境”。这种环境的核心优势在于,研究者可以精确地、系统性地调整问题的“组合复杂度”(例如增加汉诺塔的盘子数),同时保持问题底层的逻辑结构不变。这样做不仅能有效避免数据污染问题,更重要的是,它使得研究者能够像调试程序一样,检查模型生成的中间推理步骤(即“思考过程”)是否正确,从而能够更深入、更严谨地分析模型的“思维”模式、优势和根本性局限。
模型的推理能力是通用的,还是仅仅是更高级的模式匹配?它们的性能如何随问题复杂度扩展?与投入相同计算资源的标准模型相比,它们的优势何在?通过梳理文献中提到的“过度思考”(overthinking)等现象,作者将自己的研究目标聚焦于系统性地分析模型的思考量与任务复杂度的关系。
数学与谜题环境 (Math and Puzzle Environments)
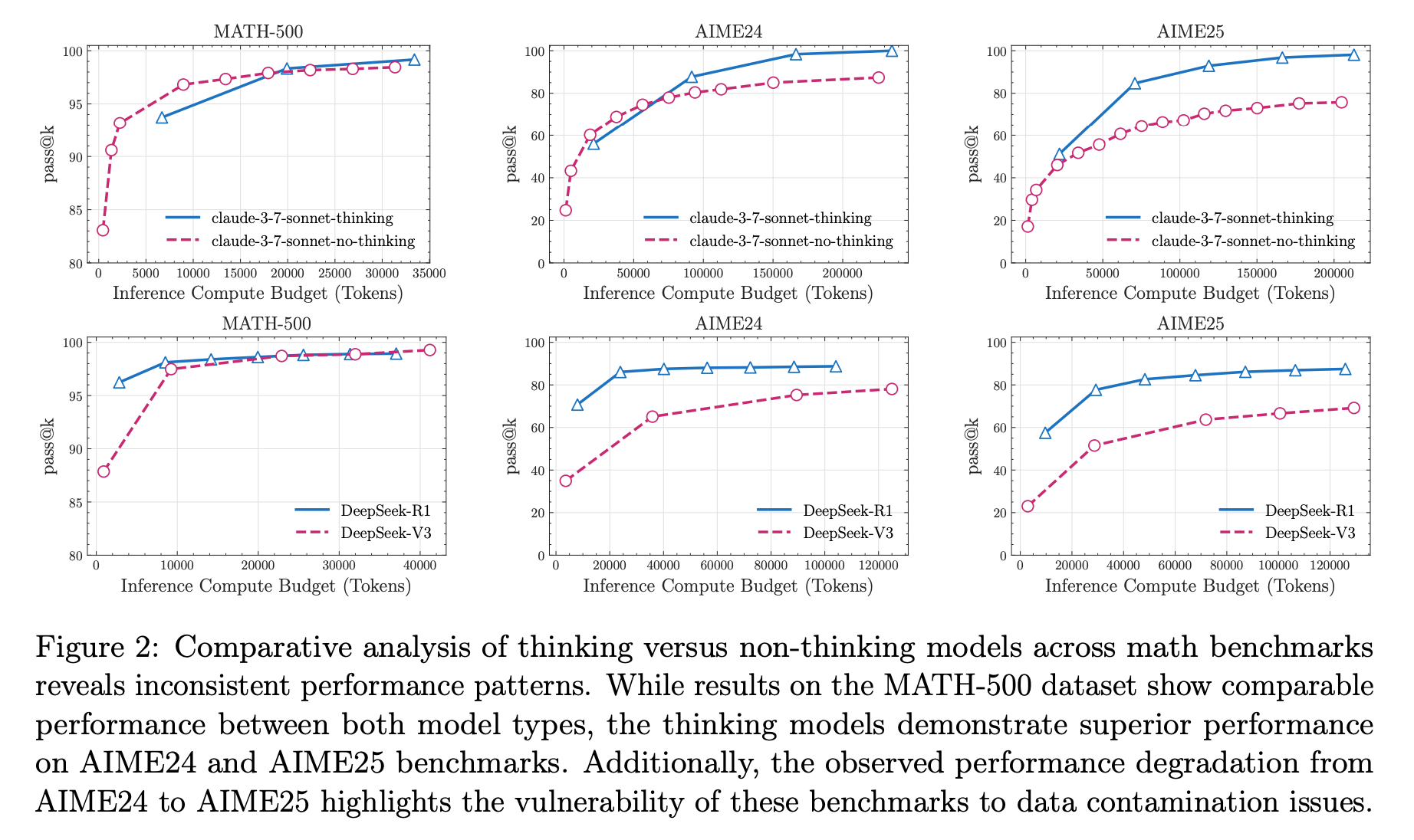
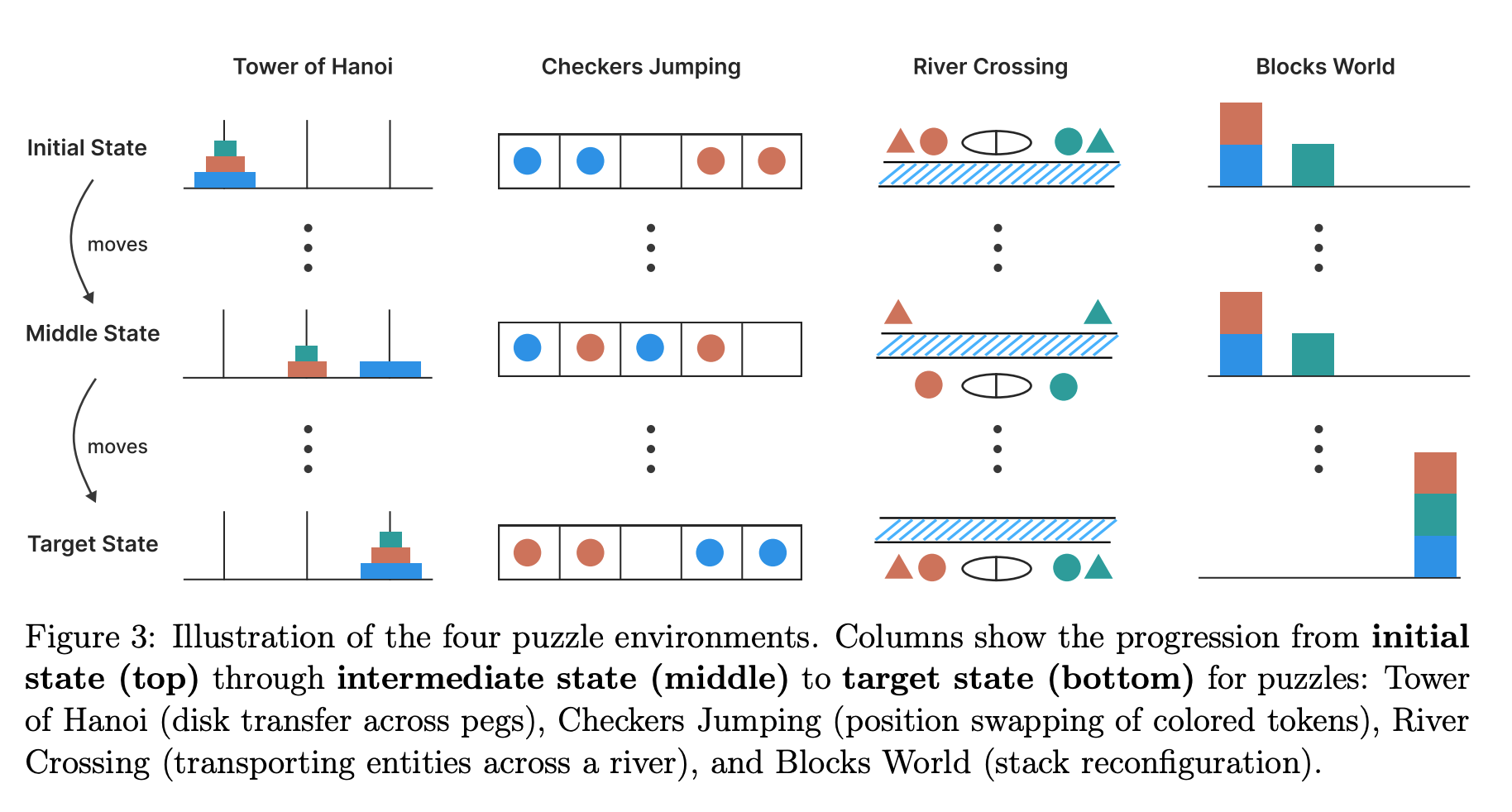
通过对比实验,论证了传统数学基准的局限性,并详细阐述了其核心研究工具——四种可控谜题环境的设计理念。首先,作者通过在MATH-500和AIME等数学基准上的实验发现,推理模型和非推理模型的性能差距并不稳定,这种不一致性可能源于更复杂的推理需求,但也极有可能是因为新基准测试的数据污染较少。这种模棱两可的结果凸显了传统基准在“控制变量”上的不足。为此,作者引入了四个精心设计的谜题:汉诺塔、跳棋、过河问题和积木世界。这些谜题的关键优势在于:(1)复杂度可控:可以通过改变盘子、棋子或积木的数量来精确调整难度,其解决问题所需的最少步数甚至有明确的数学公式,例如汉诺塔的步数是$2^{n}-1$;(2)逻辑明确:解决这些谜题仅需遵循明确给出的规则,考验的是模型的算法推理能力而非背景知识;(3)无数据污染:这些谜题的变体在网络上较少,可以避免模型通过记忆来“作弊”;(4)可验证性:可以利用模拟器对模型生成的每一步进行精确验证,从而进行细致的失败分析。这种从模糊到精确的研究工具转换为后续的深入分析奠定了基础。
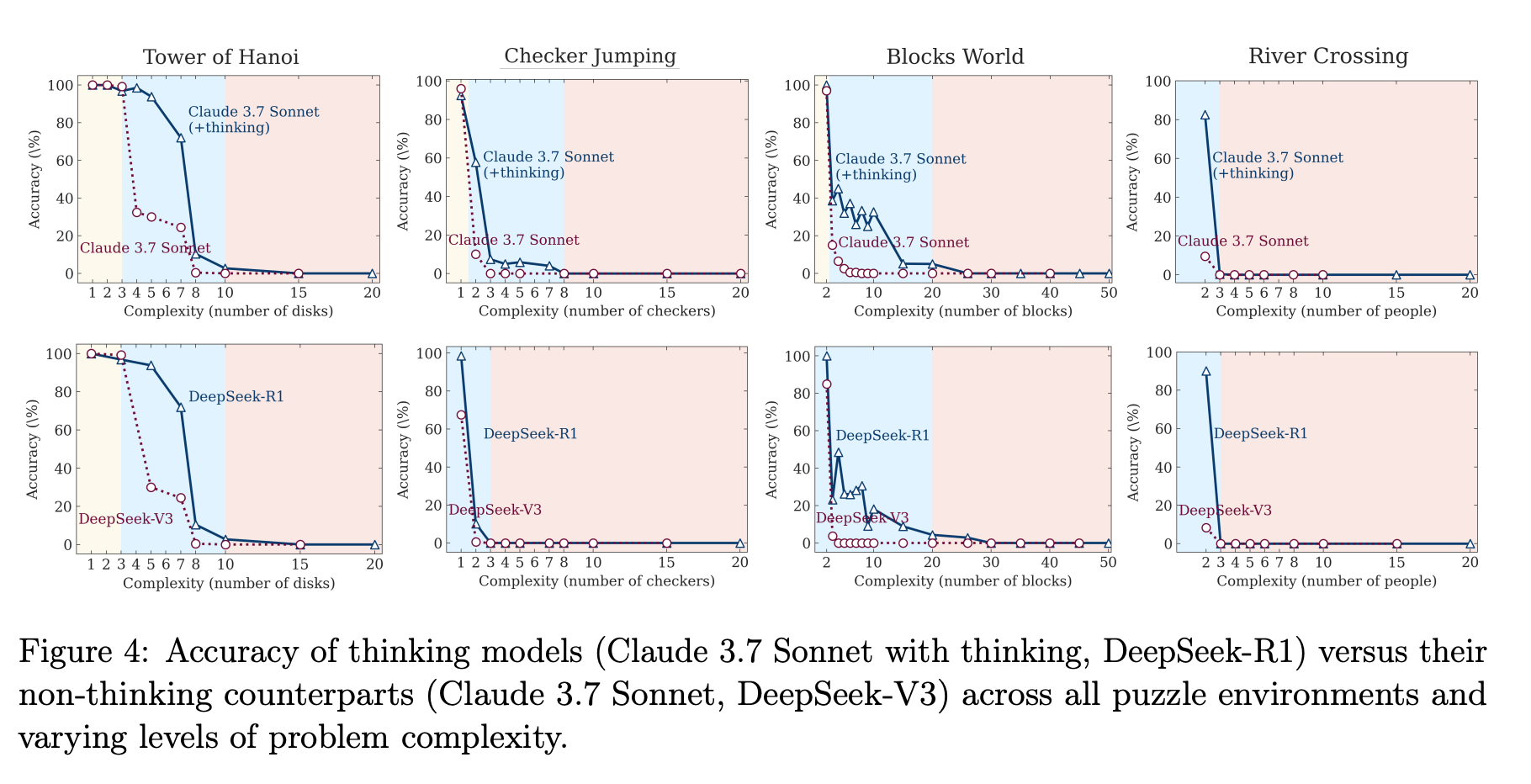
实验与结果
通过一系列精心设计的实验,系统性地揭示了推理模型的行为模式和内在局限。
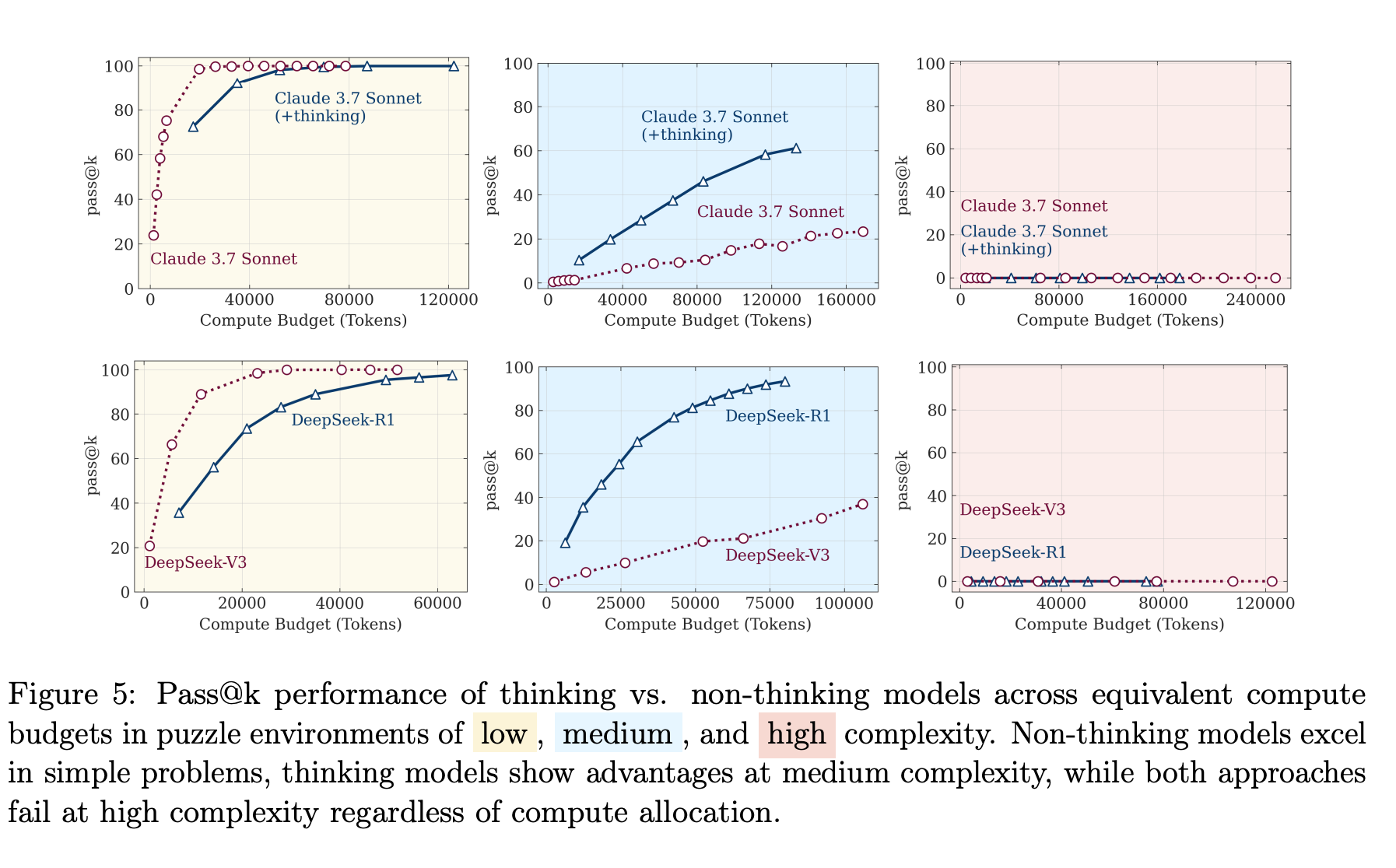
首先,通过在谜题环境中对比“思考”与“不思考”的模型,作者发现了三个清晰的复杂度区间:在低复杂度下,“不思考”的标准模型更高效准确;在中等复杂度下,“思考”模型开始展现优势;而在高复杂度下,两者性能双双崩溃。这揭示了“思考”并非万能,其有效性与任务复杂度密切相关。
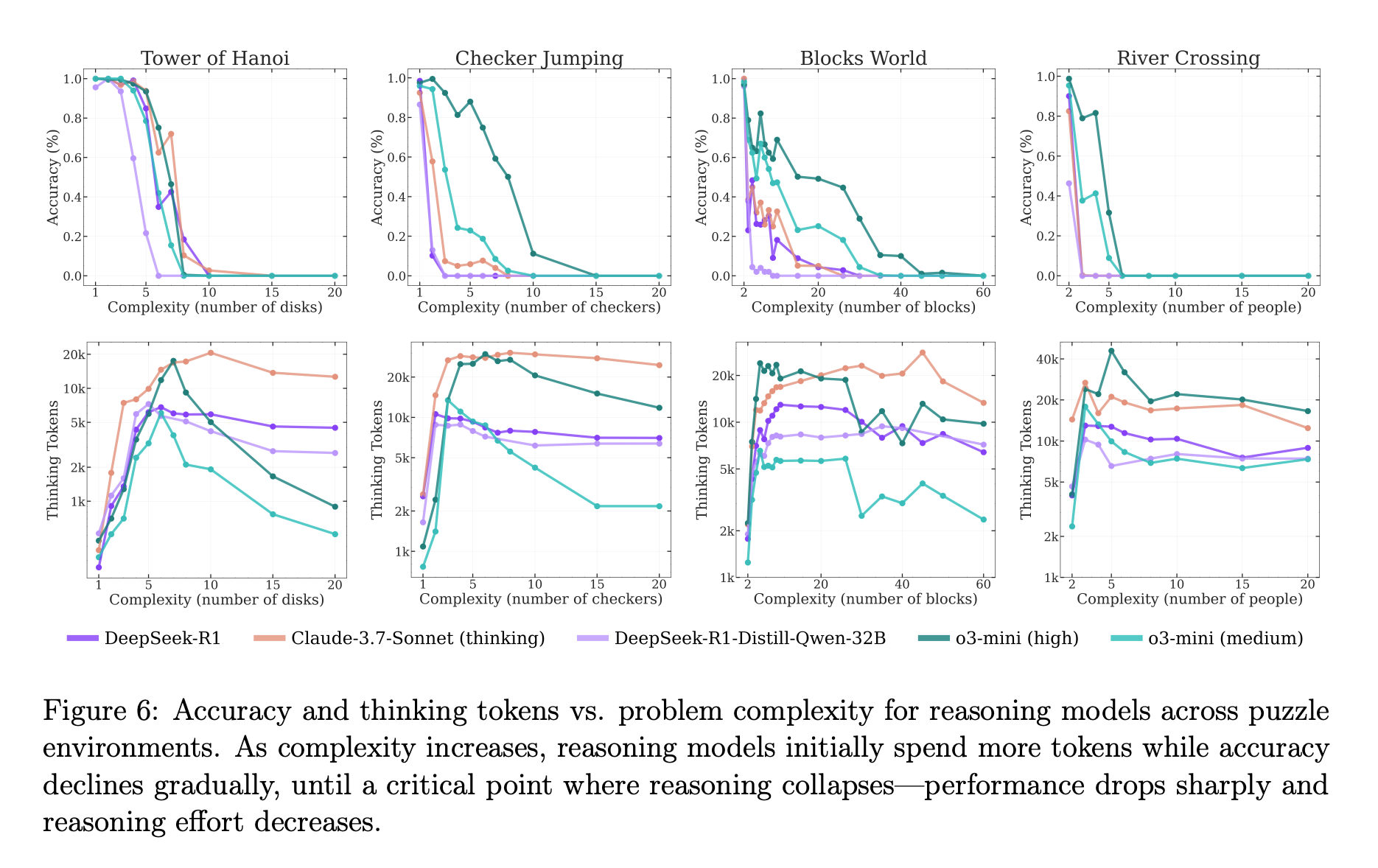
其次,研究深入分析了推理模型的“崩溃”现象。一个惊人的发现是,随着问题变得越来越难,模型的“思考投入”(以生成的token数量衡量)在达到一个峰值后便开始反常地减少,即使计算预算(token上限)远未用尽。这表明模型似乎存在一种内在的扩展限制,当它“感觉”问题过于困难时,会倾向于“放弃思考”,而不是投入更多努力。
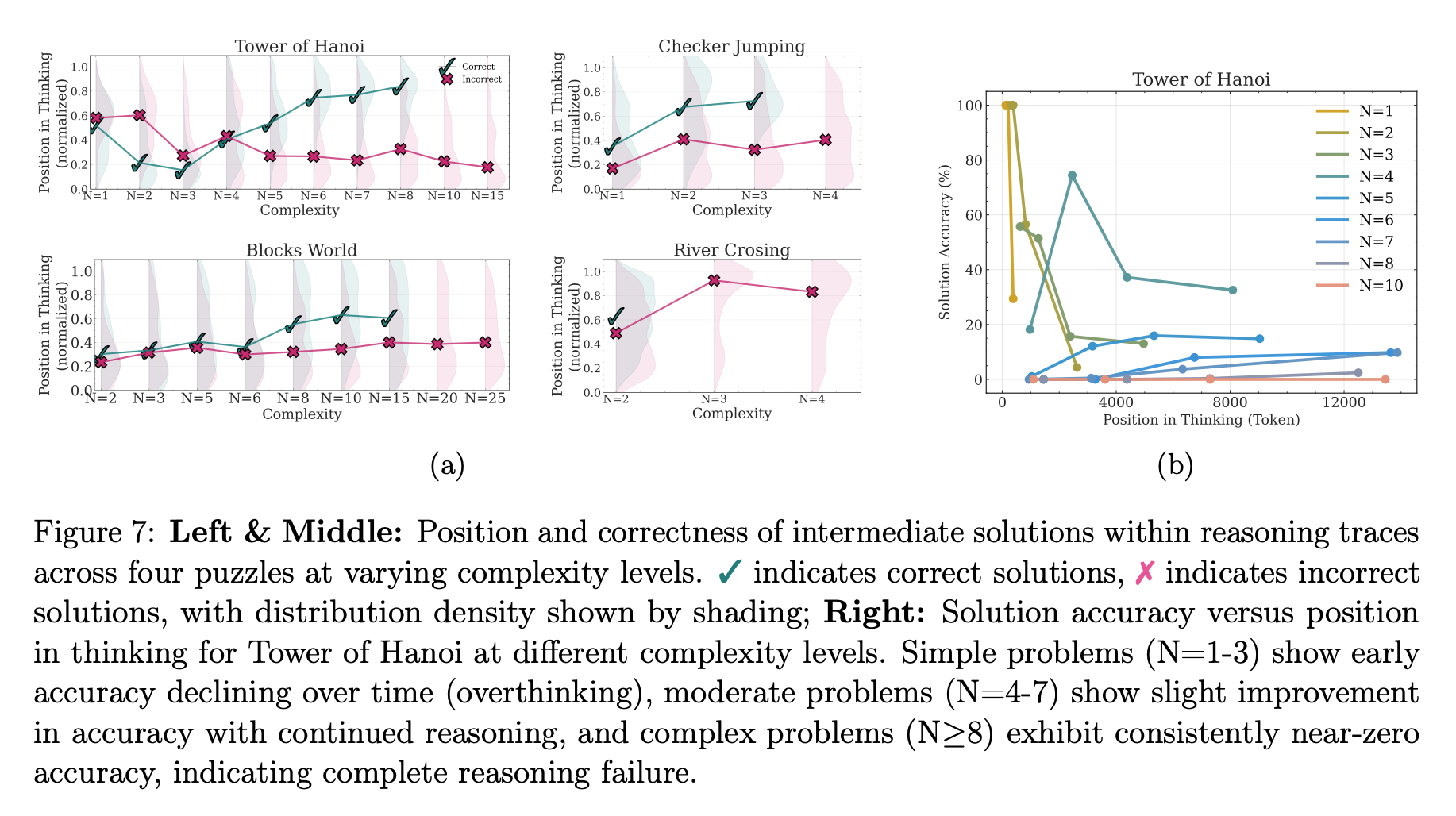
再者,作者通过分析模型“思考过程”的中间步骤,获得了更深层的洞见。他们发现,在解决简单问题时,模型会“过度思考”,即很早就找到了正确答案,但仍继续探索错误的路径,浪费计算资源。而在中等难度问题中,模型则表现出一定的“自我修正”能力,通常在探索了多个错误方案后才能找到正确答案。这一发现量化了模型的思考效率和修正能力随复杂度的动态变化。
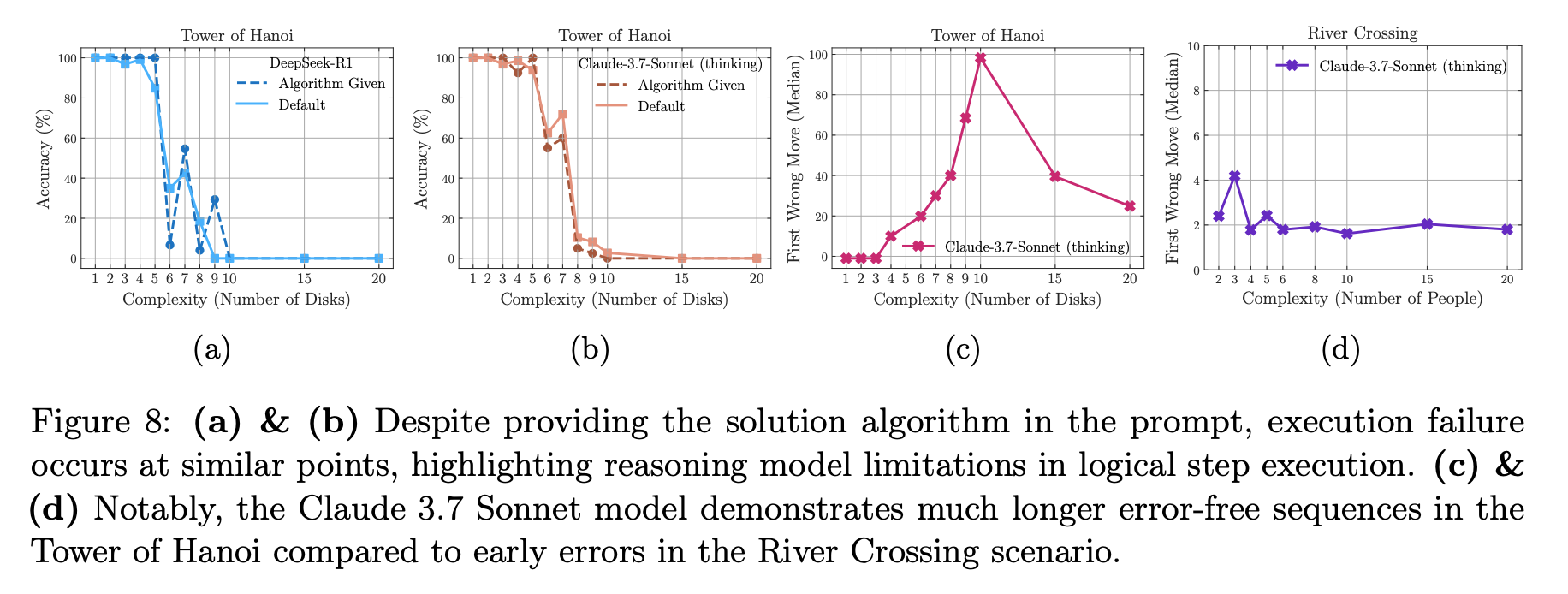
最后,作者提出了一些悬而未决的“谜题行为”。最引人深思的是,即使在提示中明确给出了解决汉诺塔问题的完整算法,模型的表现也几乎没有提升,仍然在相似的复杂度下崩溃。这强烈地暗示了当前模型在严格执行和验证逻辑步骤方面存在根本性缺陷。同时,模型在不同谜题上的表现差异巨大(例如,能解决需要上百步的汉诺塔,却在十几步的过河问题上失败),这表明其能力可能严重依赖于训练数据中的模式记忆,而非通用的、可泛化的问题解决能力。