引言

近期大语言模型的进展显著影响了人工智能中的数学推理和定理证明。尽管在自然语言领域取得了显著进步，但语言模型在形式化定理证明方面仍然面临巨大挑战，例如使用 Lean 和 Isabelle，这需要满足验证系统形式化规范的严格推导。即使是像 GPT-4 这样的先进模型，在处理复杂的形式化证明时也显得力不从心，这突显了所涉及的编码和数学的复杂性。一个形式化定理证明模型不仅必须掌握像 Lean 定理证明器这样的形式化系统的语法和语义，还必须将抽象的数学推理与精确的形式化表示对齐。

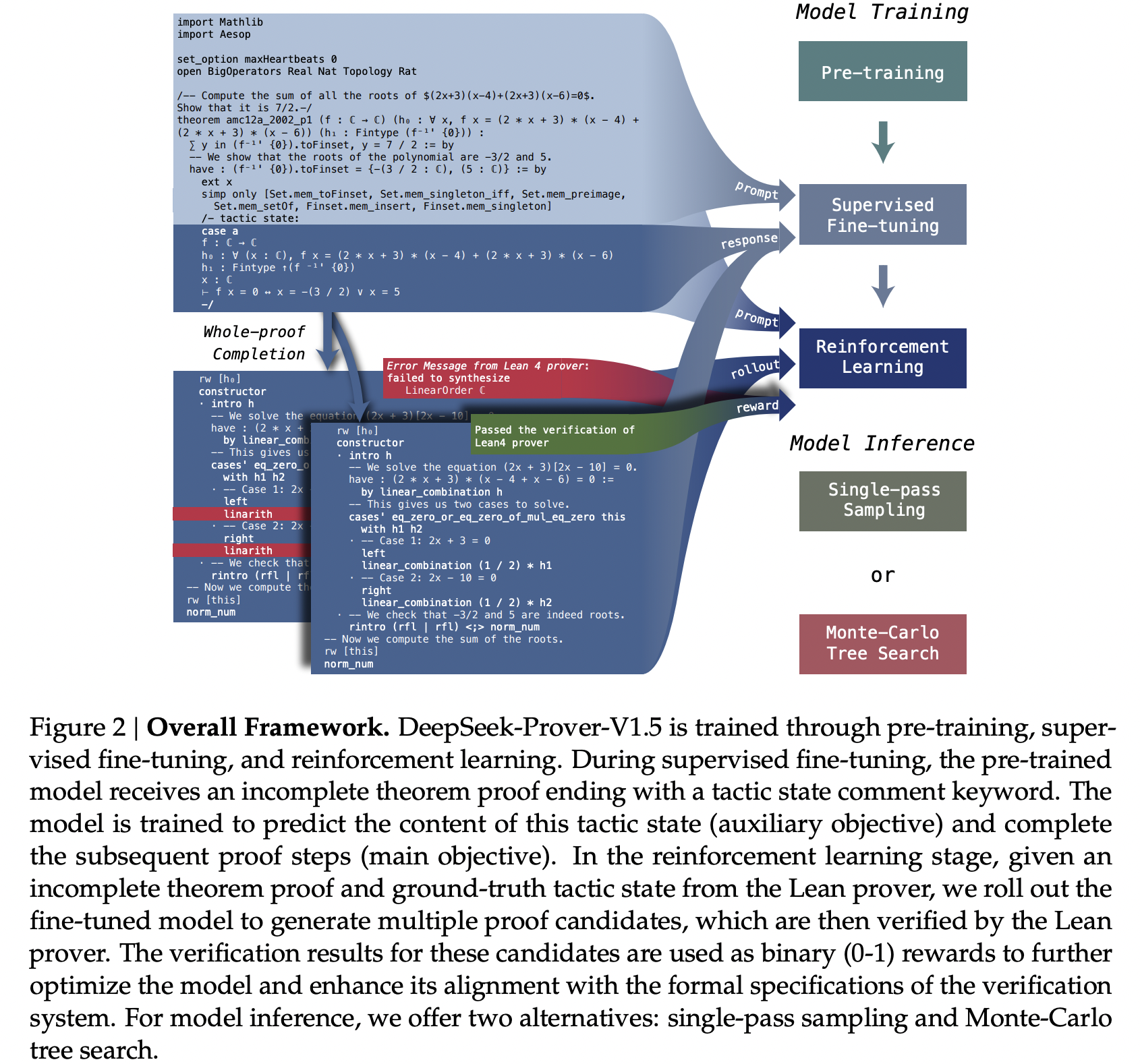
形式化定理证明中的语言模型通常采用两种策略：证明步骤生成和完整证明生成。证明步骤生成预测每个后续策略（tactic）并使用形式化验证器对其进行验证，以获取有关当前策略状态的更新信息，通常利用树搜索技术来构建有效证明。相比之下，完整证明生成计算效率高，它根据定理陈述生成整个证明代码，协调证明器模型和形式化定理验证器之间的通信预算较少。虽然 DeepSeek-Prover-V1 在 Lean 4 中通过完整证明生成取得了最先进的结果，但这种范式也带来了其独特的挑战。它需要在无法访问中间策略状态的情况下进行长序列预测，并且未来的策略依赖于这些隐藏的结果。在 Lean 的策略模式中，证明是通过一系列转换证明状态的策略来构建的。这种顺序性引入了复合错误的风险，即单个误解可能导致严重偏离有效的证明路径。更具体地说，自回归模型在生成长证明时可能对中间策略状态有错误的认知。

为了在证明步骤生成中无缝集成中间策略状态，同时保持完整证明生成的简单性和计算效率，我们在 DeepSeek-Prover-V1.5 中开发了一种统一的方法。该方法通过截断-恢复机制结合了证明步骤生成和完整证明生成技术的优点。该过程始于标准的完整证明生成，其中语言模型在定理陈述前缀之后完成证明代码。然后 Lean 证明器验证此代码。如果证明正确且完整，则过程终止。如果检测到错误，则代码在第一个错误消息处被截断，并丢弃任何后续代码。成功生成的证明代码随后被用作生成下一个证明片段的提示词。为了提高模型新补全的准确性，我们将来自 Lean 4 证明器的最新状态作为注释附加在提示词的末尾。值得注意的是，我们的方法不限于从最后成功应用的策略恢复。我们将截断-恢复机制集成到蒙特卡洛树搜索 [MCTS] 中，其中截断点由树搜索策略安排。此外，我们提出了一种新颖的用于 MCTS 的无奖励探索算法，以解决证明搜索的奖励稀疏性问题。我们赋予树搜索智能体内在动机，即好奇心（a.k.a. curiosity），以广泛探索策略状态空间。这些算法模块扩展了我们完整证明生成模型的功能，使其成为交互式定理证明的灵活工具，可以有效利用证明助手反馈并生成多样化的解决方案候选。

贡献

我们提出了一个用于开发基于语言模型的形式化数学证明器的综合框架，该框架集成了几个关键组成部分：大规模数学预训练、形式化数学语料库的构建与增强、利用证明助手反馈的在线强化学习，以及用于定理证明中长期规划的树搜索方法。预训练模型、监督微调模型、强化学习模型，以及蒙特卡洛树搜索算法的代码，均已公开，可供进一步研究和应用。

预训练：我们通过在高质量的数学和代码数据上进行进一步预训练，重点关注 Lean、Isabelle 和 Metamath 等形式化语言，以增强我们基础模型在形式化定理证明和数学推理方面的能力。
监督微调：我们通过实施两种数据增强技术来改进 Lean 4 代码补全数据集。首先，我们使用 DeepSeek-Coder V2 236B 为 Lean 4 代码标注自然语言思维链注释，从而将形式化定理证明与自然语言推理对齐。其次，我们在 Lean 4 证明代码中插入中间策略状态信息，使我们的模型能够有效利用编译器反馈。然后，使用生成的数据集对预训练模型进行微调。
强化学习：我们采用 GRPO 算法，利用证明助手反馈（RLPAF）对监督微调模型进行强化学习。Lean 证明器提供的验证结果作为奖励监督信号，增强了模型与验证系统形式化规范的对齐。
蒙特卡洛树搜索：我们通过引入一种新颖的抽象及其对应的搜索算法，推进了形式化定理证明中的树搜索方法。我们提出的截断并恢复机制作为一种状态-动作抽象，将树搜索过程无缝集成到完整证明生成框架中。我们推出了 RMaxTS，这是一种创新的蒙特卡洛树搜索算法，它利用 RMax 策略来解决稀疏奖励证明搜索问题中的探索难题。通过分配内在奖励，该算法鼓励证明器智能体生成多样化的规划路径，从而促进对证明空间的广泛探索。

评估和指标总结

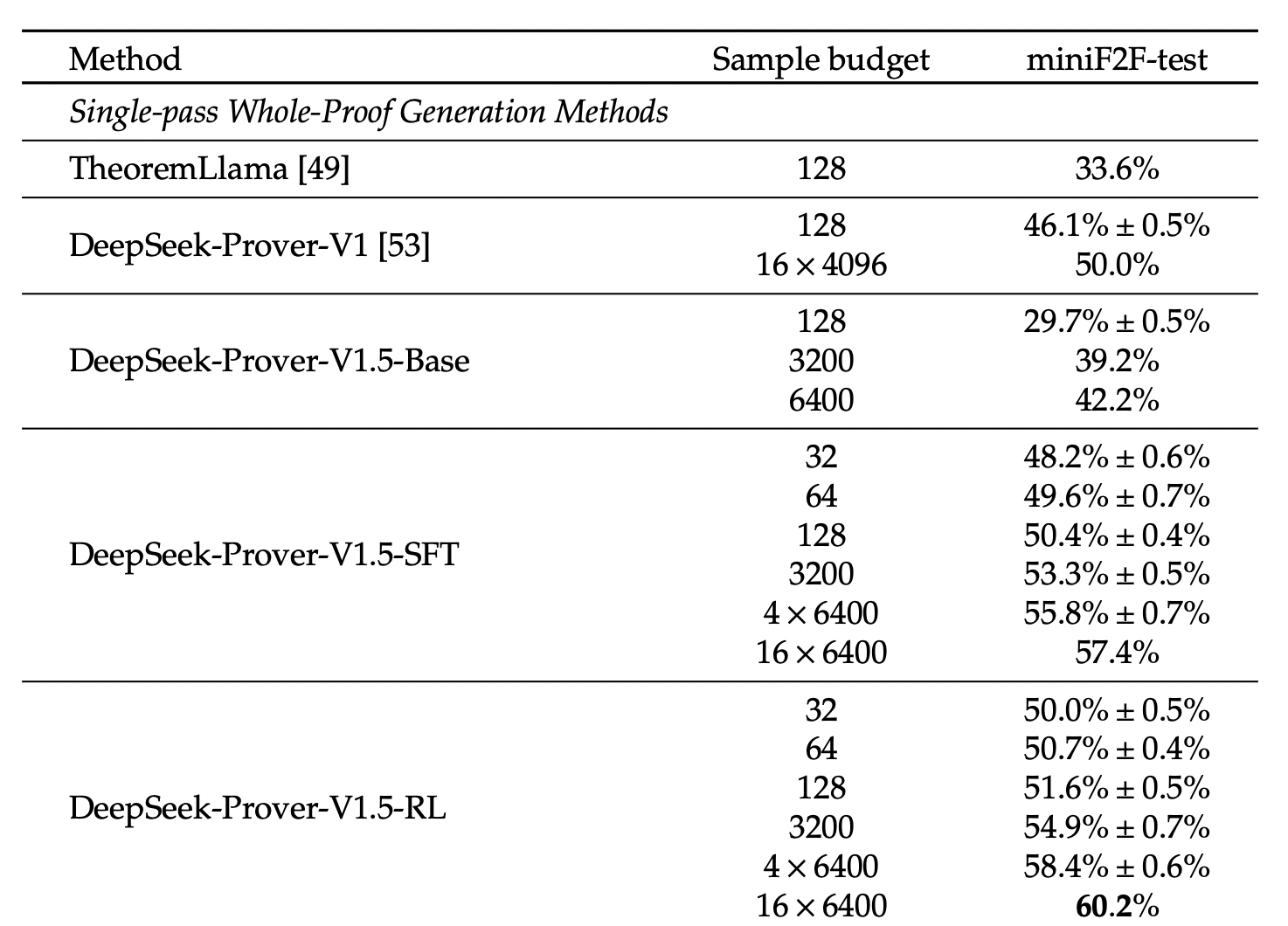
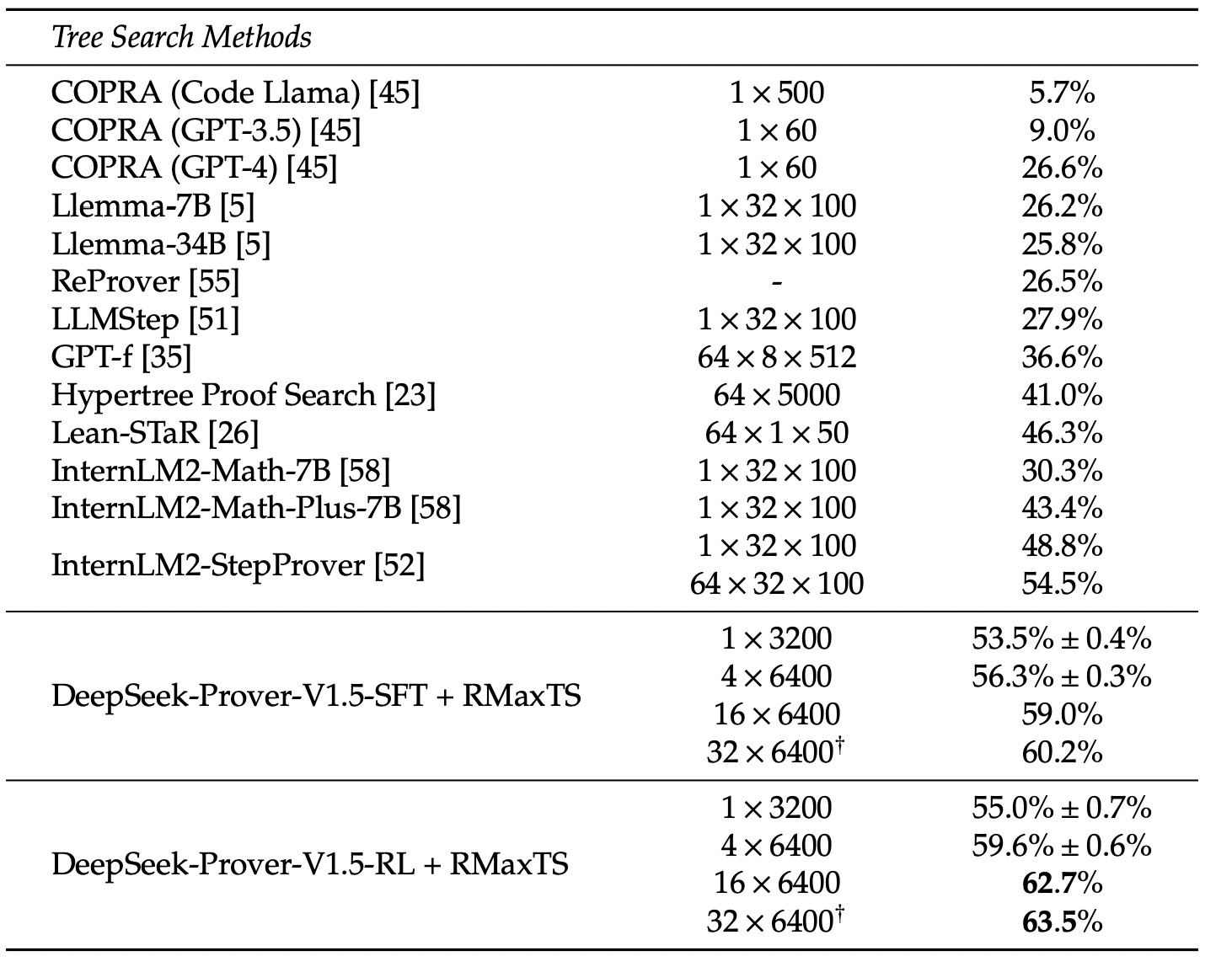
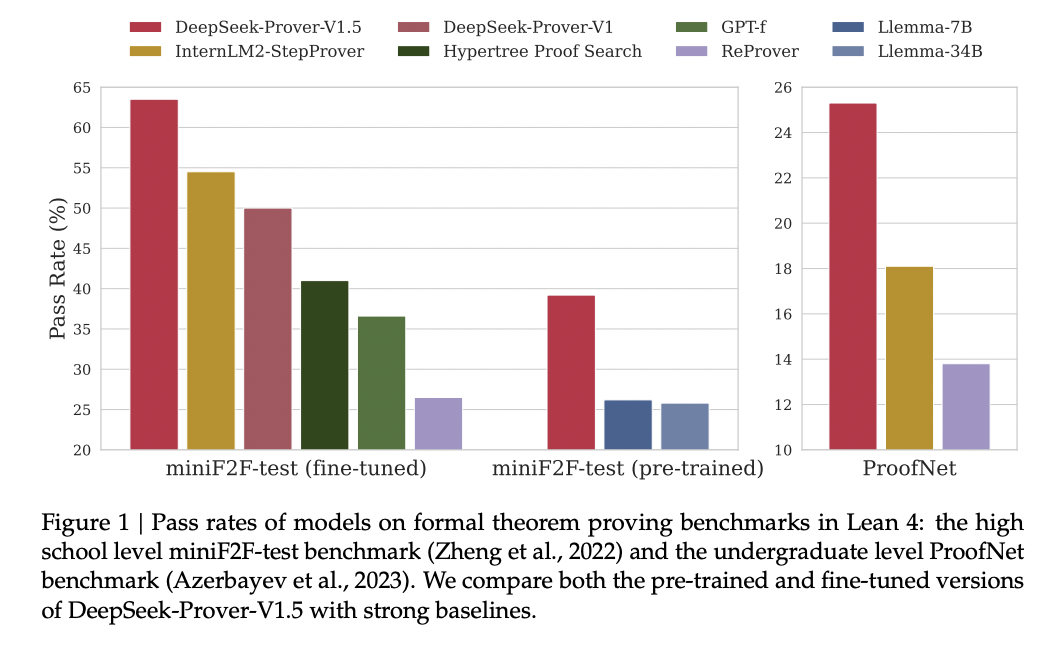
miniF2F：在单次完整证明生成设置下，DeepSeek-Prover-V1.5 在 miniF2F 测试集上实现了 60.2% 的通过率，相较于 DeepSeek-Prover-V1 的 50.0%，绝对提升了 10.2 个百分点，这是一个显著的进步。结合树搜索技术后，通过率进一步提升至新的最先进水平 63.5%。
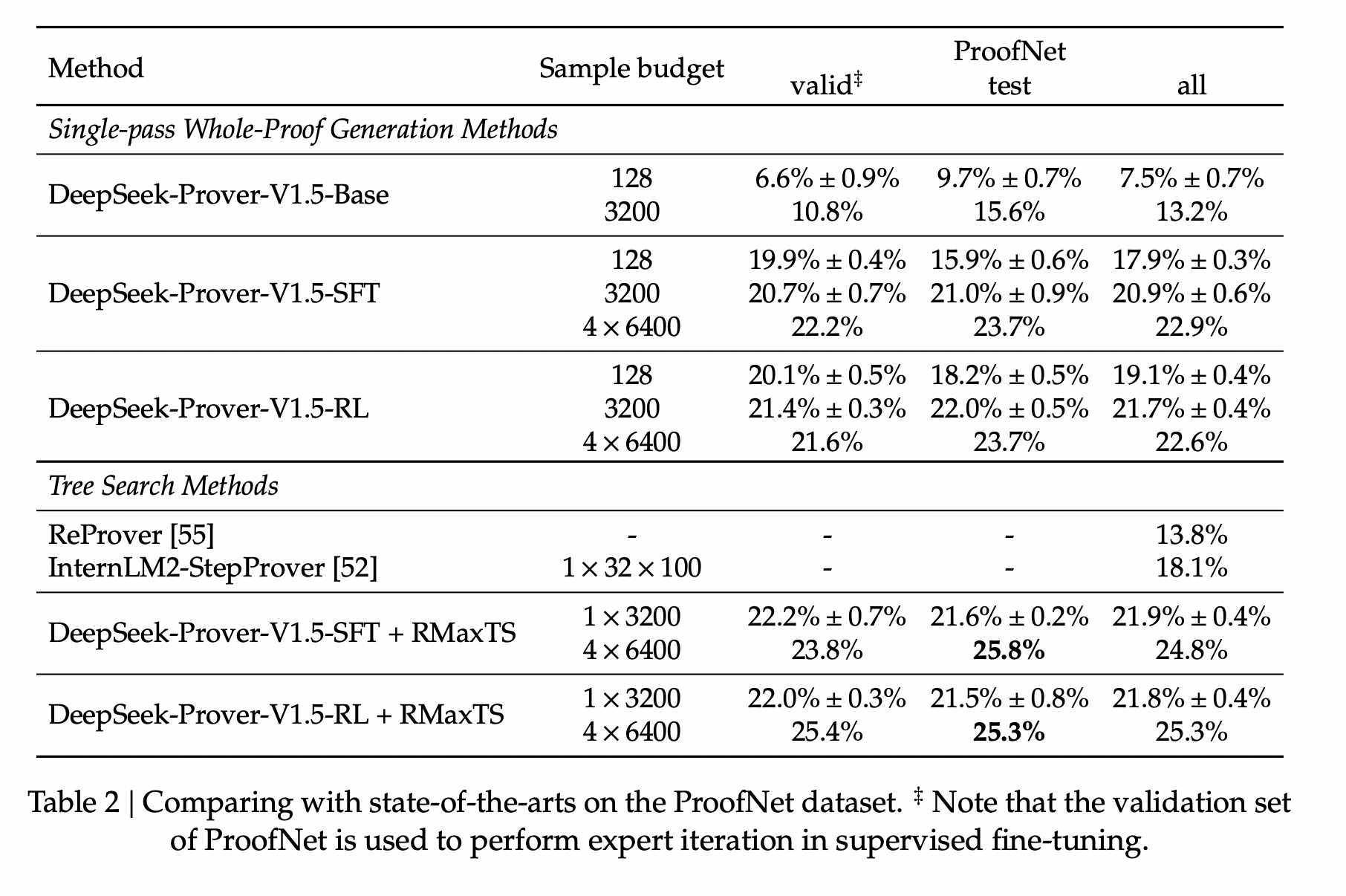
ProofNet：DeepSeek-Prover-V1.5 在 ProofNet 的单次完整证明生成设置下同样表现出强大的性能，其验证集通过率为 21.6%，测试集通过率为 23.7%。集成树搜索技术进一步提升了这些结果，在验证集上达到了 25.4% 的新最先进通过率，在测试集上达到了 25.3% 的新最先进通过率。

预训练

为了增强我们语言模型在生成形式化证明和通过数学语言进行推理方面的熟练度，我们进一步对我们的基础模型进行了预训练。这一改进涉及在包含代码和自然语言数学内容的高质量数据集上进行训练。我们特别关注了在证明助手中广泛使用的形式化语言，例如 Lean、Isabelle 和 Metamath。我们将这个改进后的模型命名为 DeepSeek-Prover-V1.5-Base。

监督微调

在本节中，我们探讨了 DeepSeek-Prover-V1.5 监督微调 (SFT) 所涉及的方法论和过程。具体而言，我们通过添加详细的解释性注释来扩充来自 DeepSeek-Prover-V1 的证明数据集。此增强旨在改善自然语言描述与 Lean 4 代码之间的对齐，从而促进更好的形式化数学推理。此外，我们引入了中间策略状态信息作为一项辅助预测任务，以支持蒙特卡洛树搜索过程中使用的截断与恢复机制。我们将最终得到的模型称为 DeepSeek-Prover-V1.5-SFT。

数据整理

我们为监督微调开发了一个全面的 Lean 4 代码补全数据集。该数据集包括从广泛的形式化定理中衍生的合成证明代码。这些定理来源于各种项目，例如标准的 Lean 4 数学库 Mathlib4、来自 DeepSeek-Prover-V1 和 Lean Workbook 的合成定理，以及来自 miniF2F 和 ProofNet 基准测试的验证集。为了扩充形式化证明数据，我们采用了一个专家迭代过程。这包括使用语言模型生成证明，验证生成的证明数据，用验证过的数据重新训练模型，然后使用优化后的模型生成额外的证明数据。在每次迭代之间，我们使用 DeepSeek-Coder V2 236B 在证明代码前以注释的形式标注思考过程。最后，我们为蒙特卡洛树搜索的截断-恢复机制定制了这些数据。最终的证明数据集包含 9,645k 个序列。

思想增强的证明生成

在 DeepSeek-Prover-V1 中，我们识别出自然语言的问题解决策略与 Lean 中的定理证明之间存在显著的差距。在自然语言场景下，模型会生成详细的推导步骤来构建证明；而在 Lean 环境中，模型通常依赖一系列高级策略调用来强行求解。这些高级策略虽然有效，但其内部工作机制和结果并不透明，这阻碍了模型运用结构化数学推理来解决复杂证明目标的能力。为应对此问题，我们开发了一种在生成定理证明代码前融入自然语言推理的方法。该方法类似于 Lean-STaR 在每个证明步骤前执行独立的思维链推理，但我们的方法将这种推理直接作为注释整合进证明代码中。我们利用 DeepSeek-Coder V2 236B，通过两种方式增强 DeepSeek-Prover-V1 中的现有数据：一是在证明块的起始位置插入完整的自然语言解题步骤；二是为相应的 Lean 策略交替插入具体的自然语言步骤说明。使用这种数据格式训练模型，能够促使模型在证明块开始时提出完整的数学推理思路，并在执行每个策略前进行详细的步骤规划。此方法成功地引导模型形成了新的行为模式，即运用精细的数学思维来指导策略的生成。在训练数据中，我们使用了两种不同的指导性提示词，以区分证明代码补全任务中的 CoT（思维链）模式与非 CoT 模式。

使用策略状态信息增强提示词

为了实现蒙特卡洛树搜索（Monte-Carlo Tree Search）的截断-恢复机制，我们需要从模型生成的代码中提取策略（tactic）信息。我们利用 LeanDojo 项目的数据提取工具，对 Lean REPL [读取-求值-打印循环；@repl] 进行了增强。这使我们能够以三元组的形式提取策略信息，其中包括每个策略的位置，以及其应用前后的策略状态（tactic states）。这些信息有助于我们识别出引发验证错误的具体策略代码。对于生成的有效形式化证明中的每一个策略，我们会插入验证器返回的策略状态，形式为注释“/- tactic state: … -/”。在训练过程中，我们将“/- tactic state: ”之后的所有 Token 用作响应（response）来计算监督微调（supervised fine-tuning）损失，而此注释之前的 Token 则用作提示词（prompts），不参与训练损失的计算。

训练设置

我们基于预训练模型进行监督式微调 (supervised fine-tuning)，训练数据量为 90 亿 Token，使用的批量大小 (batch size) 为 2048，恒定学习率为 1e-4。训练过程包含 100 个预热 (warm-up) 步骤以稳定学习动态。训练样本被随机拼接以形成序列，最大上下文长度为 4096 个 Token。

来自证明助手反馈的强化学习

强化学习（RL）已被证明能有效增强经过监督微调的语言模型的数学推理能力。为了进一步提升 DeepSeek-Prover-V1.5-SFT，我们引入了一个强化学习阶段，从而产生了 DeepSeek-Prover-V1.5-RL 模型。此阶段利用强化学习（RL），根据来自 Lean 4 证明器的验证反馈来提升性能。该强化学习（RL）过程的具体细节将在下文详述。

提示词

在强化学习阶段，我们使用来自监督微调数据集的一个定理陈述子集作为训练提示词。我们选择那些 DeepSeek-Prover-V1.5-SFT 在多次尝试中生成正确证明具有中等成功率的定理。这确保了模型既有改进的空间，同时仍能够接收到正反馈。经过筛选后，我们保留了大约 4.5k 条独特的定理陈述。每个定理都添加了 CoT 和非 CoT 指导提示词作为前缀，以增强模型在这两种模式下的证明生成能力。

奖励

当通过强化学习 (RL) 训练大语言模型时，通常由一个训练好的奖励模型提供反馈信号。相比之下，形式化定理证明受益于证明助手对所生成证明进行的严格验证，这是一个显著优势。具体而言，每个生成的证明如果被验证为正确，则获得奖励 1，否则为 0。尽管这种二元奖励信号是准确的，但它也相当稀疏，特别是对于那些对监督微调模型而言具有挑战性的定理。为缓解这种稀疏性，我们选择那些对监督微调模型既有挑战性又可实现的训练提示词，如上文所述。

强化学习算法

我们采用组相对策略优化 [GRPO] 作为我们的强化学习算法，该算法已被证明比 PPO 更有效和高效，主要是因为它消除了训练额外评论家模型的必要性。具体来说，GRPO 为每个定理提示词采样一组候选证明，并根据组内输出的相对奖励来优化模型。我们的提示词选择策略旨在使得候选证明中很可能同时包含正确和错误的证明，这与 GRPO 的组相对特性非常契合，从而增强了训练过程。

训练设置

我们基于 SFT 模型进行强化学习（RL）训练，该模型同时用作初始模型和施加库尔贝克-莱布勒（KL）散度惩罚的参考模型。我们使用 5e-6 的恒定学习率，KL 惩罚系数设置为 0.02。对于每个定理，我们采样一组 32 个候选证明，最大长度设置为 2,048。训练批次大小配置为 512。

基准测试

我们在以下基准测试上评估定理证明性能，以比较模型在每个训练阶段后的能力：

MiniF2F 专注于高中水平练习和竞赛（如 AMC、AIME 和 IMO）的形式化问题解决能力，重点是代数和数论。该基准测试包括 244 个验证问题和 244 个测试问题，最初使用 Lean 3 编写，并基于 @minif2f_solution 提供的版本手动转换为 Lean 4.9.0。
ProofNet 评估本科数学水平的形式化定理证明能力。它包含来自广泛使用的本科教科书的 185 个验证问题和 186 个测试问题，涵盖实分析与复分析、线性代数、抽象代数和拓扑学。这些问题最初使用 Lean 3 编写，并手动转换为 Lean 4.9.0。

提示词配置

对于 DeepSeek-Prover-V1.5-Base 的每次证明尝试，我们从验证集中独立采样三个证明示例来构建少样本学习提示词。对于 miniF2F 基准，我们使用来自 @minif2f_solution 的人工编写的证明，而对于 ProofNet 基准，我们使用由 DeepSeek-Prover-V1.5-RL 生成的正确证明作为少样本学习示例。对于 DeepSeek-Prover-V1.5-SFT 和 DeepSeek-Prover-V1.5-RL，我们采用了两种类型的引导提示词：一种在每个证明步骤之前鼓励思维链 (CoT) 推理，另一种则不鼓励 (non-CoT)。

指标

我们使用 pass@$K$ 准确率指标来评估定理证明性能，该指标衡量模型在 $K$ 次尝试内生成正确证明的成功率。每个模型部署在单个 A100-40G GPU 上，利用 vLLM 框架进行样本生成。采样参数设置为温度为 1，top-p 值为 0.95，以及最大 Token 限制为 2,048。生成的证明随后使用 Lean 4 定理证明器进行验证。为了进行此验证，我们导入 Mathlib4 和 Aesop 以访问预定义的前提和策略。验证过程的时间限制为 300 秒。

各训练阶段比较

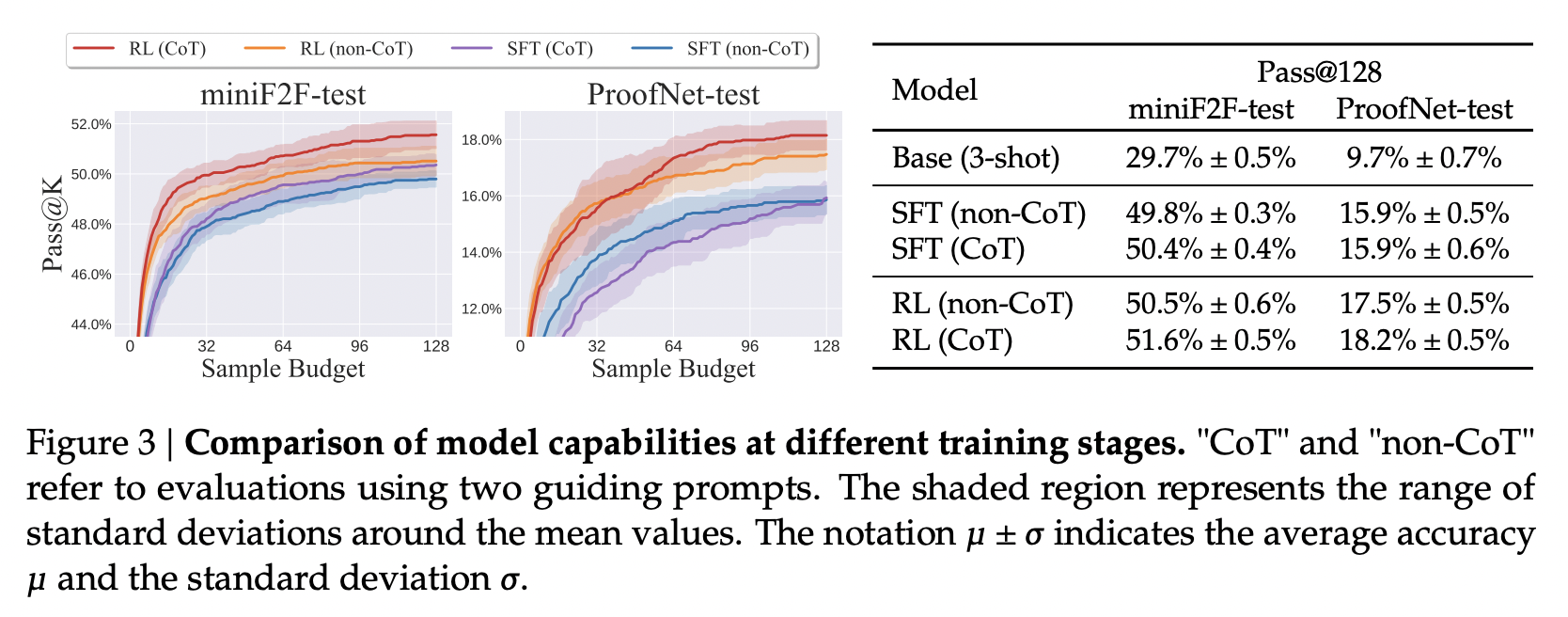
图3展示了在 miniF2F 和 ProofNet 数据集上每个训练阶段的比较分析。我们的基础模型 DeepSeek-Prover-V1.5-Base 取得了显著的通过率，在 miniF2F 基准测试集的测试中，使用三样本提示解决了近三分之一的问题。监督微调阶段产生的 DeepSeek-Prover-V1.5-SFT 显著优于基础模型，在 miniF2F 上的 Pass@128 准确率提升了约三分之二，在 ProofNet 上则翻了一番。随后的强化学习阶段进一步提升了模型的性能，提高了所有 $K$ 值下的 Pass@$K$ 准确率。与自然语言数学领域的研究发现（例如 DeepSeekMath 报告的结果）不同——在那些研究中强化学习主要提升了 TopK 中的正确响应——我们观察到在形式化定理证明中基础能力得到了真正的增强。这种改进不仅在小样本预算下显而易见，而且随着样本预算的增加也保持稳定。

CoT 与非 CoT 的比较

我们比较了 DeepSeek-Prover-V1.5-SFT 和 DeepSeek-Prover-V1.5-RL 这两种模型在非 CoT 和 CoT 生成模式下的性能。图3中的结果表明，在大多数设置中，CoT 模式的表现始终优于非 CoT 模式。具体而言，DeepSeek-Prover-V1.5-RL 利用这些增强的定理证明模式，在两个基准测试上均取得了更优越的性能，其在 miniF2F 上的平均准确率为 $51.6\%$，在 ProofNet 上的平均准确率为 $18.2\%$。CoT 模式中对自然语言推理的整合，显著增强了形式化证明写作的规划与执行能力。

Tactic-level Tree Abstraction

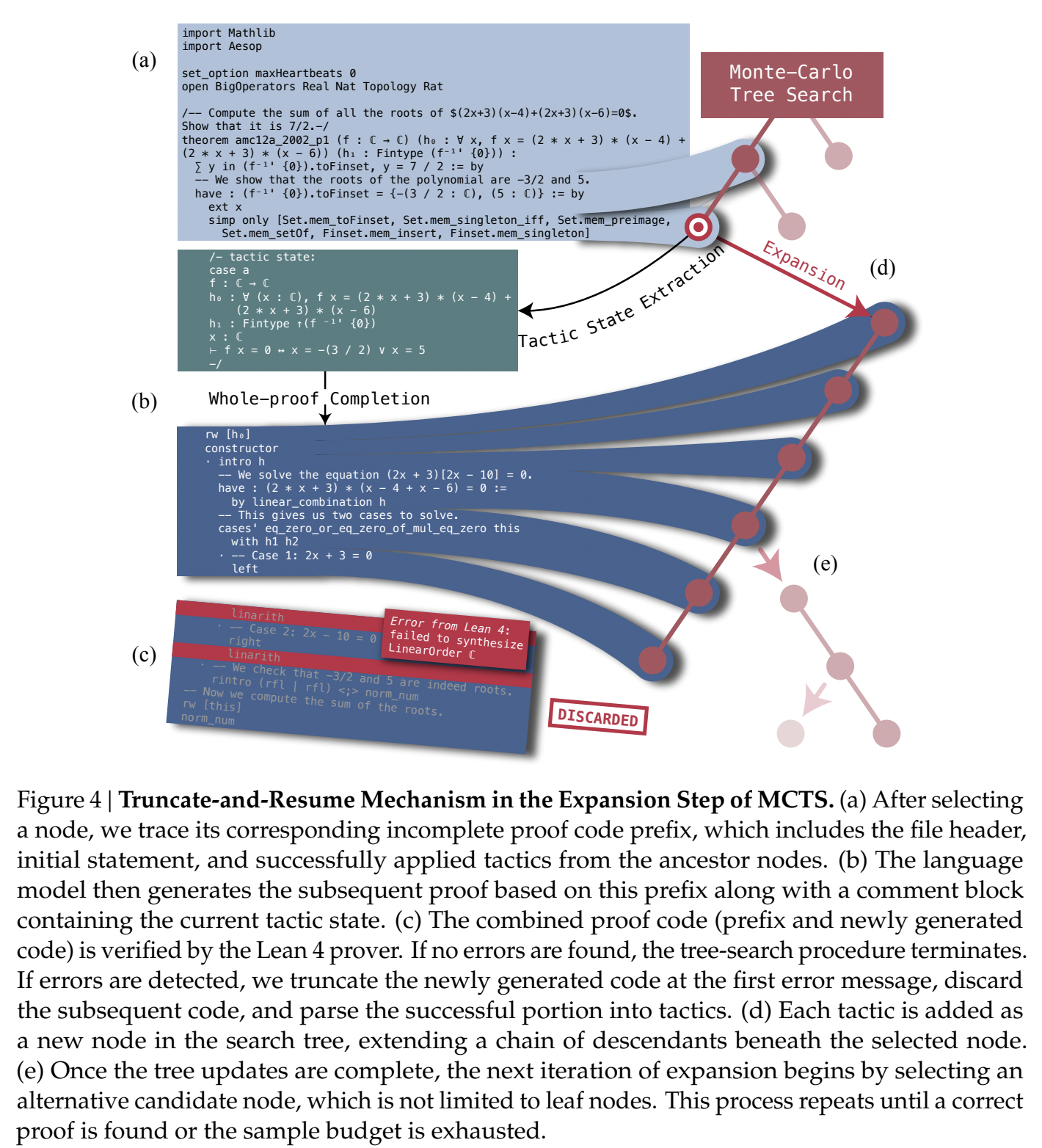
为了在完整证明生成的场景下应用树搜索方法，我们引入了一种证明树抽象，它利用截断并恢复机制来定义定制化的状态与动作空间。大致遵循 @yao2023tree 的范式，我们首先将一个不完整的证明分解为一系列对应于单个证明步骤的树节点，然后利用存储在这些树节点中的部分内容来继续证明生成过程。图4展示了在完整证明生成过程中构建证明搜索树的过程。

截断：将证明分解为树节点

我们在策略层面构建证明搜索树，其中每个树边代表策略状态的单个转换步骤。最初，我们将模型生成的整个证明提交给 Lean 证明器，将其解析成策略。然后，我们在最早出现的验证错误处截断证明，确保所有后续的策略代码都能成功应用，以推动证明向目标定理前进。策略代码被分割成若干代码片段，每个片段包含一个有效的策略代码及其相关的思维链注释，对应于代表策略状态转换的单个树边。通过这种抽象，每个策略代码被转换成一系列树节点，形成一条从根节点到特定节点的路径。

恢复：从树节点生成证明

在 Lean 4 中，不同的策略（tactic）可以导致相同的策略状态（tactic state），这意味着我们证明树（proof tree）中的每个节点可以对应于一组达成相同结果的不同策略代码。为处理此情况，我们在每个节点存储一组这些等效的策略代码。当树搜索智能体（tree search agent）扩展一个节点时，它会随机选择一个策略用作语言模型（language model）的提示词（prompt）。此提示词包含以所选策略结尾的不完整证明代码，以及来自 Lean 证明器（Lean prover）的策略状态信息（作为一个注释块）。经过微调（fine-tuned）的模型已被训练来识别并利用此格式，使用经策略状态注释增强的不完整代码来指导后续的证明生成。

通过蒙特卡洛树搜索进行交互式定理证明

我们的证明搜索树是使用标准的蒙特卡洛树搜索 (MCTS) 范式 [MCTS] 开发的，该范式迭代地应用四个步骤：选择、扩展、模拟和反向传播。我们将模拟步骤整合到扩展中，因为我们的全证明生成模型固有地从扩展节点执行推演。算法工作流程的详细设计如下。

选择

$$ \begin{aligned} \label{eq:tree_policy} TreePolicy(s) = \mathop{\arg\max}_{a\in Children(s)\cup\{\oslash\}} Q_{UCB}(s, a), \end{aligned} $$

其中动作 $a$ 可以是移动到子节点（表示为 $a\in Children(s)$），也可以是扩展当前节点 $s$（表示为一个特殊 Token $a=\oslash$）。这种方法使用了一种称为虚拟节点（virtual node）的技术，它为每个节点分配一个假想的子节点，用以代表选择当前节点 $s$ 进行扩展。这使得树搜索智能体能够持续扩展非叶节点，因为其动作空间由一个生成式模型支持，该模型的输出范围无法通过固定次数的试验来确定。在节点 $s$ 上执行动作 $a$ 的值估计 $Q_{UCB}(s,a)$ 由两个部分组成：

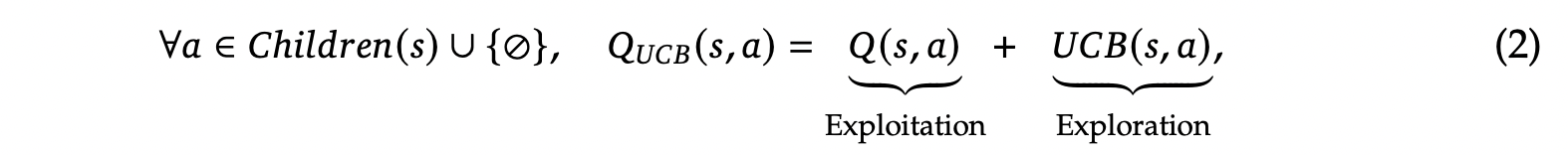
其中 $Q(s, a)$ 表示从选择历史中派生出的、基于样本的动作值估计，作为利用（exploitation）部分，用于从之前的试验中检索高价值的候选者。$UCB(s, a)$ 表示通过上置信界（Upper Confidence Bounds, UCB）[@auer2002using] 计算得出的探索奖励（exploration bonus），该奖励随着状态-动作对 $(s,a)$ 的重复执行而减少。更具体地说，$Q_{UCB}(s, a)$ 代表对 $Q(s, a)$ 的一个乐观估计，并且可以大概率地作为其上界。

扩展

下一步是调用证明生成模型来扩展在选择阶段被指定的节点。从指定用于扩展的节点中，我们恢复其存储的不完整证明代码，执行全证明生成来提出一系列后续策略，并将生成的证明提交给 Lean 证明器进行验证。这种完成证明的尝试，等同于在标准 MCTS 框架内进行单次模拟推演（rollout of simulation）。当验证结果表明证明已完成时，搜索过程便可以终止，因为已为目标定理找到了新的证明。若未完成，我们则解析验证反馈，并将生成的证明截断到出现第一个验证错误的那步断言。剩余的策略被转换为一个节点路径，并合并到搜索树中（参见图4）。必须指出，由于我们采用的是全证明生成设置——其输出是包含一连串策略的完整证明，而非仅仅是下一步策略——因此，我们的扩展过程可能在每次迭代中向搜索树插入一个由节点组成的路径。这与为竞技类游戏设计的传统 MCTS 不同，后者通常在每次迭代中仅扩展一层子节点。

反向传播

每次树搜索迭代的最后阶段是沿着从根节点到扩展节点选择轨迹更新价值统计数据，即，更新与公式1所述的树策略相关的值。令 $\tau=\{(root, s^{(1)}), (s^{(1)}, s^{(2)}), (s^{(2)}, s^{(3)}), \dots, (s^{(|\tau|-1)}=s_t, \oslash)\}$ 表示第 $t$ 次迭代的选择轨迹，该轨迹以 $s_t$ 作为扩展节点结束。我们通过考虑最近的轨迹奖励 $R(\tau)$ 来更新所有 $(s,a)\in\tau$ 的 $Q_{UCB}(s,a)$（详情参见公式7）。奖励的外部来源来自编译器反馈，具体来说，为已完成的证明分配奖励 $R_{\text{extrinsic}}(\tau)=1$，为未解决的证明分配奖励 $R_{\text{extrinsic}}(\tau)=0$。我们将介绍一种内在奖励机制来增强奖励分配，从而提高智能体的探索动机。

蒙特卡洛树搜索的内在奖励

在形式化定理证明的搜索问题中，外在奖励极其稀疏，即，搜索智能体只有在证明完全解决时才能获得非零奖励。更具体地说，证明搜索过程形成了一个树状结构，其中只有一小部分叶节点能带来非零奖励，这与统计强化学习文献中一个著名的困难探索案例相符。为了在稀疏奖励的序贯决策中促进探索，一个经典的范式是构建内在奖励，这种奖励不仅鼓励智能体优化外在奖励，还鼓励其获取关于交互环境的一般信息。在本节中，我们提出了我们的由内在奖励驱动的探索算法，应用于树搜索的 RMax (RMaxTS)，旨在将无奖励探索整合到证明搜索问题中。

RMax 应用于 MCTS

我们采用经典的探索机制 RMax，为蒙特卡洛树搜索 (MCTS) 构建内在奖励。RMax 的核心思想是探索并广泛覆盖状态空间。当智能体到达一个未曾访问过的状态时，会给予自身最大额度的奖励。在证明搜索的背景下，系统在证明完成前不提供任何外在奖励，此时我们的算法流程类似于 ZeroRMax：智能体的探索完全由内在奖励驱动，即设 $R(\tau)=R_{\text{intrinsic}}(\tau)$。一次树扩展步骤的内在奖励取决于是否有新节点被添加到搜索树中：

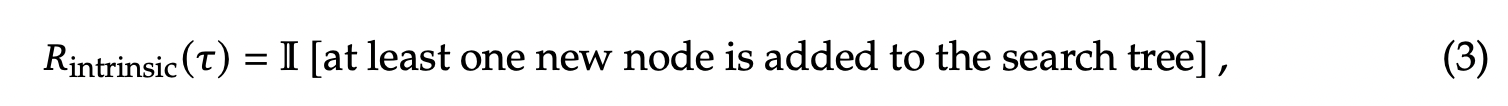
其中 $\tau$ 表示最近一次需要为其分配奖励以进行反向传播的选择轨迹。这种探索策略优先扩展那些节点，在这些节点上，证明器模型生成的策略能够引导至多样化的策略状态。由于多个不同的 Lean 代码可能导致相同的中间状态转换，这种启发式方法有望减少冗余生成并提高样本效率。

针对非平稳奖励的 UCB

蒙特卡洛树搜索中 UCB 探索奖励的常见设置是使用 UCB1：

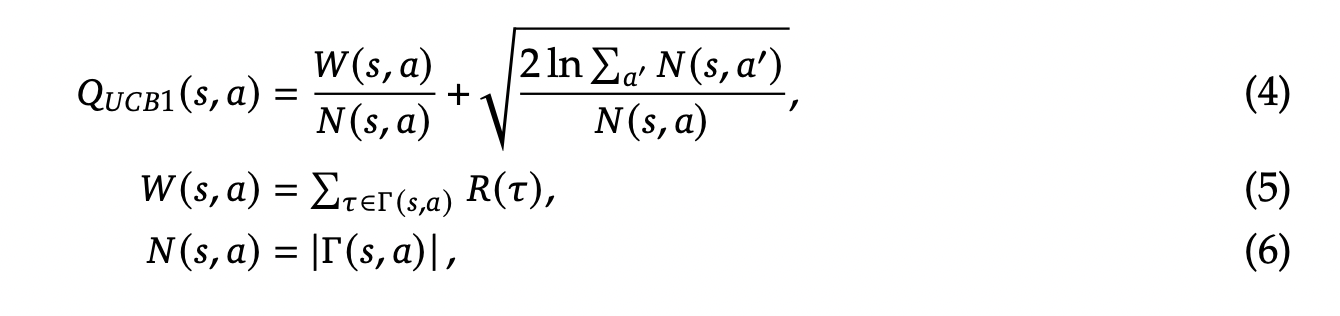
其中 $\Gamma(s,a) = \{\tau\mid (s,a)\in\tau\}$ 表示包含 $(s,a)$ 作为中间选择步骤的树策略轨迹 $\tau$ 的列表。为方便讨论，我们将列表 $\Gamma(s,a)=\{\tau_1,\tau_2,\cdots\}$ 进行组织，使得新收集的轨迹具有更大的下标索引。在这项工作中，我们建议使用 UCB 方法的一个替代变体。请注意，公式3中推导出的内在奖励是一个非平稳奖励信号，其期望值随着探索的进展而衰减。这是因为随着搜索树通过复杂的探索而扩展，发现具有未见过的策略状态的新节点无疑变得更加困难。为了解决非平稳性问题，我们考虑折扣置信上限 [DUCB; @garivier2011upper]，它使用一个折扣因子 $\gamma\in(0,1)$ 来平滑地降低那些过时反馈记录的影响：

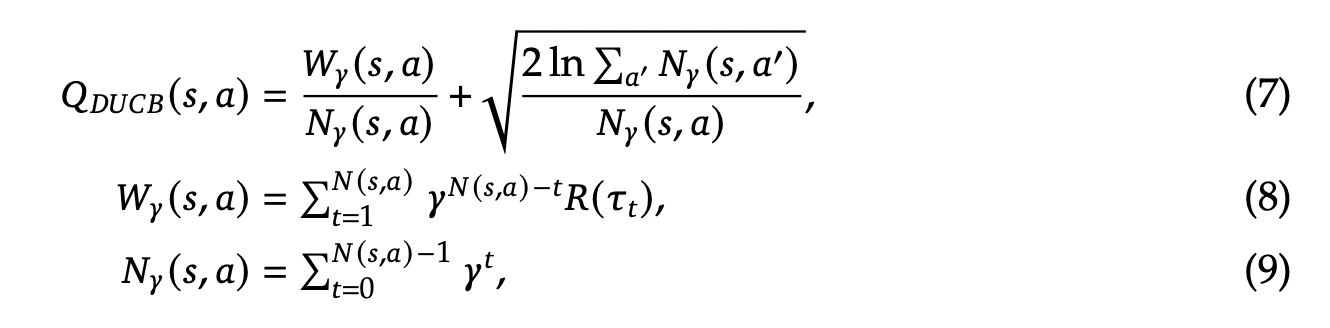
其中新收到的反馈将在价值估计中被赋予更大的权重。在实践中，我们设置 $\gamma=0.99$。请注意，DUCB 中的折扣因子 $\gamma$ 的作用不同于其在无限视界马尔可夫决策过程 (MDP) 的价值迭代中的作用。该折扣应用于树搜索的迭代，而不是单个轨迹内的动作步视界。

蒙特卡洛树搜索的并行化

为了提高蒙特卡洛树搜索（MCTS）的效率，我们实施了 @chaslot2008parallel 所描述的几种成熟的并行化技术。

- 根并行化： 我们为每个节点部署 256 个 MCTS 运行器，每个 GPU 配备一个语言模型，用于证明生成的批量大小为 512。Lean 证明器通过 REPL 调用，并在一个拥有数千个 CPU 核心的集群上执行，其中每个证明验证任务由一个在沙盒中创建和终止的独立进程处理。语言模型的证明生成和 Lean 证明器的验证均异步处理。这种设置允许 MCTS 运行器执行并发树搜索操作，从而显著加速整个过程。

- 树并行化： 我们为每个搜索树配置 32 个线程工作器，以并行化树的迭代步骤。此方法有效地调度并平衡了证明生成和 Lean 验证的任务。每个线程工作器迭代地执行树搜索循环：选择一个候选节点进行扩展，调用语言模型生成证明，使用 Lean 证明器验证生成的证明，并执行反向传播。

- 虚拟损失： 为了鼓励并发的线程工作器选择多样化的节点，我们为当前进行的迭代分配一个虚拟奖励 $R(\tau)=0$。这包括暂时反向传播一个值为 $0$ 的奖励，并在迭代完成后将其更新为真实奖励。该策略促进了对不同扩展节点的探索，进而提高了整体搜索效率。

与现有方法的比较

在本节中，我们将我们提出的证明树搜索方法（该方法引入了一种新颖的用于完整证明生成的截断-恢复机制）与现有方法进行比较。当前在形式化数学证明搜索中使用语言模型的方法通常分为两种主要策略：

- 多遍证明步骤生成：此策略将证明过程分解为策略生成和验证的多个阶段，通常遵循树搜索模式。它涉及一次生成和验证一个策略，然后为下一个策略重复该过程，直到没有证明目标为止。著名的例子包括 GPT-f、Thor、ReProver、Hypertree Proof Search 和 InternLM2-StepProver。

- 单遍完整证明生成：此方法尝试一次性生成并验证整个证明。如果证明不正确，模型将在下一次尝试中生成新的证明。此类方法包括 DSP、Subgoal-Prover、LEGO-Prover、Lyra 和 miniCTX。

我们的证明树搜索方法独特地结合了这两种策略，提供了一种新颖的混合方法。它以完整证明生成开始，类似于单遍方法，但通过实现复杂的截断-恢复机制对其进行了扩展。此过程涉及将生成的证明截断为其成功的初始段，将此段解析为单独的策略，并从该点恢复树搜索。这种迭代过程有效地实现了蒙特卡洛树搜索，无缝地将单遍完整证明生成与多遍证明步骤生成相结合。因此，我们可以用几乎相同的目标来训练一个单一模型，使其能够同时支持这两种策略。我们的实验结果表明，这种统一的方法在两种设置下均表现出更优越的性能。通过结合现有方法的优点并引入创新技术，我们的方法为形式化数学证明搜索提供了一种更通用、更有效的解决方案，有望为该领域的未来发展铺平道路。

实验结果

在本节中，我们使用两个不同的基准来评估 DeepSeek-Prover-V1.5 的定理证明能力：miniF2F，其包含高中水平的练习题和竞赛题；以及 ProofNet，其涉及本科水平的定理。我们展示了完整证明生成和蒙特卡洛树搜索方法的结果。

DeepSeek-Prover-V1.5：利用证明助手反馈进行强化学习和蒙特卡洛树搜索

引言

贡献

评估和指标总结

预训练