《SRPO: A Cross-Domain Implementation of Large-Scale Reinforcement Learning on LLM》
摘要
以OpenAI的o1和DeepSeek的R1为代表的推理模型最新进展,凸显了强化学习在提升大语言模型推理能力方面的显著潜力。然而,由于方法论的透明度不足,这些技术突破在不同领域的复现仍面临挑战。本研究提出两阶段历史重采样策略优化(Two-Staged history-Resampling Policy Optimization, SRPO),该方案在AIME24和LiveCodeBench基准测试中,使用与深度求索相同的基础模型(即Qwen2.5-32B),仅通过强化学习(无需预先监督微调/Supervised Fine-Tuning)便超越了DeepSeek-R1-Zero-32B的性能表现。基于组相对策略优化(Group Relative Policy Optimization, GRPO)框架,我们创新性地提出:(1)跨领域两阶段训练范式——平衡数学推理与编程能力的协同发展;(2)历史重采样(History Resampling, HR)技术——针对训练过程中低效样本的优化方案。大量实验证实了该方法的有效性,为扩展大语言模型在多任务场景下的推理能力提供了重要洞见。
引言
具体来说,我们实施了一个两阶段训练范式来培养 大语言模型 (LLM) 的推理和领域特定技能。我们发现,尽早增强长思维链 (CoT) 推理能力对于跨任务泛化至关重要。在第一阶段,我们主要使用数学数据进行训练,以培养反思性思维和逐步解决问题的能力。在第二阶段,我们整合编码数据,建立在第一阶段培养的推理技能基础之上。这种范式确保了推理和编码能力的稳步提升。
为了解决 GRPO 中的零优势现象(该现象阻碍了梯度更新并降低了样本效率),我们引入了历史重采样。通过过滤掉持续正确的答案,我们确保了有意义的梯度,提高了样本效率,并加速了收敛。
此外,我们详细介绍了我们的数据策展流程,包括数据清洗和难度级别分类。最终的训练数据集使模型接触到具有挑战性的高质量问题,旨在培养复杂的推理能力。
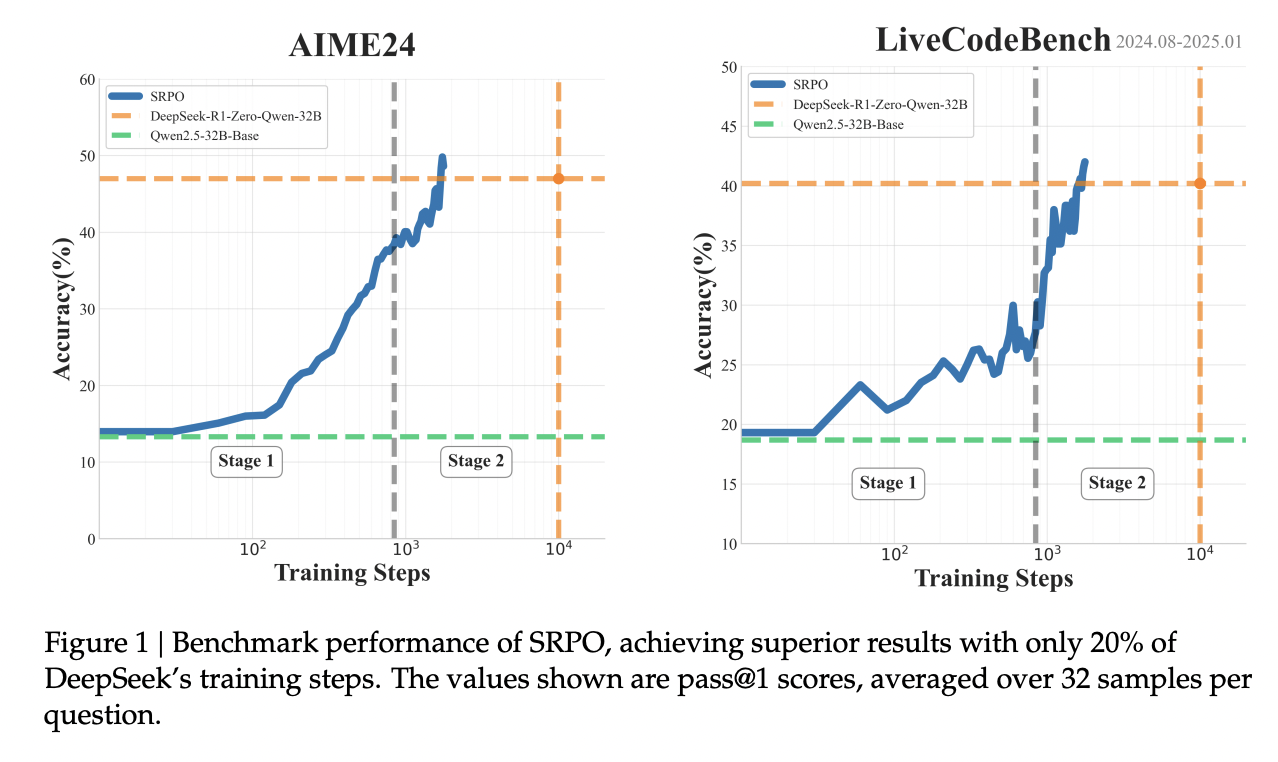
结合上述技术,SRPO 在 AIME24 上达到了 50.0 pass@1,在 LiveCodeBench 上达到了 41.6 pass@1,超过了 DeepSeek-R1-Zero-Qwen-32B 的性能(在 AIME 上为 47.0 分,在 LiveCodeBench 上为 40.2 分),且仅用了 2,000 步——仅为 R1-Zero 训练步数的 1/5。
GRPO
GRPO 的核心思想是通过一组 rollout 内的相对奖励来估计基线。因此,它降低了 critic 模型的计算成本并提高了训练稳定性。具体来说,对于每个问题 q,模型生成一组响应 $o_1, o_2,... , o_G$ 并计算相应的奖励 $r_1, r_2, ... , r_G$。$A_i$ 是通过在每个组内对奖励进行归一化而获得的优势。
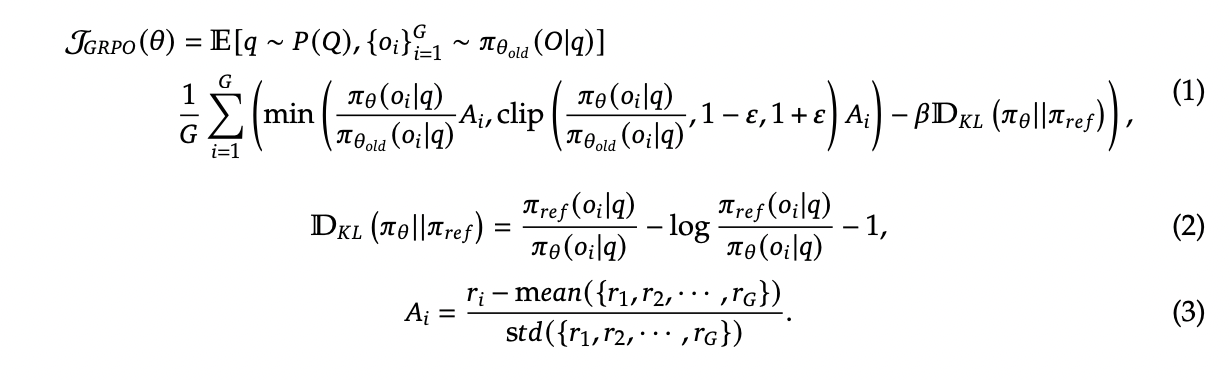
训练模板
为了可复现性,我们采用了 DeepSeek-R1-Zero 中指定的训练模板,如图2所示。该模板既不提供明确的反思性推理提示,也不提供具体的解题策略,从而确保模型完全依靠其内在的推理能力来解决问题。
对于包含起始代码的代码问题,我们将问题描述和起始代码提供的函数名称整合到相应的问题中。
使用 Vanilla GRPO 实现时遇到的挑战
在我们使用 vanilla GRPO 训练 Qwen-2.5-32B-Base 基础模型的初步实验中,我们遇到了几个训练瓶颈,这些瓶颈阻碍了模型在数学和代码基准测试中达到预期的 R1-Zero 性能。这些挑战包括:
- 数学和代码之间固有的响应长度冲突: 我们发现数学问题通常会引发更长、更细致的逐步推理模式(长 CoT),而对代码数据进行强化学习(RL)训练并不鼓励模型生成更长的响应。直接混合这两种类型的数据会产生固有的冲突,限制了模型针对数学推理优化发展必要的详细阐述能力,或是针对编码任务优化发展偏好的简洁表达能力。因此,这种冲突导致了在两个领域中的次优性能。
- 因组内奖励相同而导致的训练效率下降: GRPO 算法依赖于采样组内的非零奖励方差来计算优势(Eq.3)。当一个组内的所有或大多数模拟运行(rollouts)产生相同的奖励值时,计算出的优势接近于零。因此,当训练批次中的大部分出现这种现象时,有效的梯度贡献变得微乎其微,从而显著阻碍了训练效率。
- 过早的性能饱和: GRPO 训练在评估基准测试中经常遇到性能平台期,其特点是奖励改善过早放缓。这个问题通常源于数据集质量不足。具体来说,当训练数据缺乏足够的复杂性或多样性时,特别是如果过于简单的问题占主导地位,模型倾向于保守地维持其在这些较容易任务上的性能。因此,它难以进行更具挑战性问题所需的更深入和扩展的推理过程,从而限制了其推理能力的整体发展。
两阶段训练
为应对数学和代码之间内在的响应长度冲突这一挑战,我们提出了一种两阶段训练范式:
阶段 1(激发推理能力): 初始训练阶段仅专注于具有挑战性的数学数据。此阶段的目标是旨在促进扩展的思维链(CoT)能力的形成,包括反思性停顿、回溯行为和逐步分解。
阶段 2(技能整合): 在此阶段,将代码数据引入训练过程。基于阶段 1 建立的推理基础,此阶段旨在让模型熟练掌握代码生成技能。除了直接提升代码能力外,此阶段也旨在引导模型掌握程序化思维、递归和工具调用能力。
训练策略的比较分析
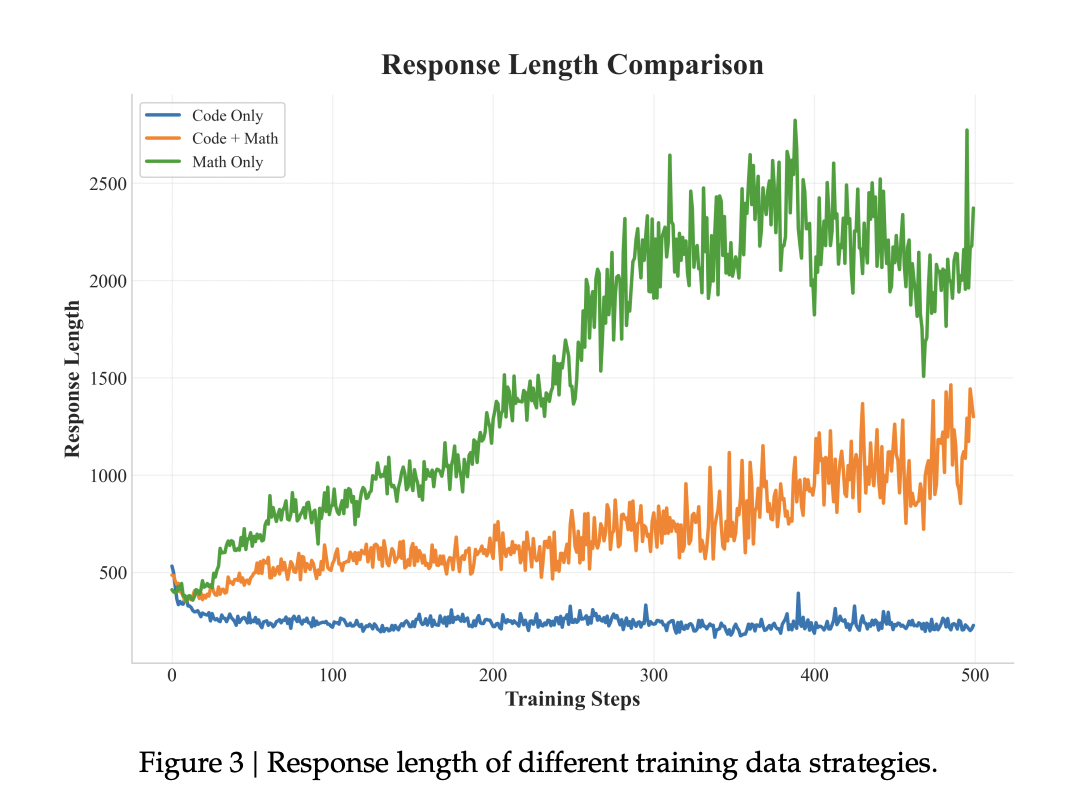
图3展示了不同训练策略下响应长度的增长情况。为了验证我们的分阶段训练方法,我们进行了比较研究,分析了不同训练范式下的推理行为和性能。
混合训练
直接在数学和代码数据的混合体上训练的模型,在响应长度增长方面表现有限,并且基准测试性能较差。案例研究揭示了不一致的推理模式:虽然数学问题能引发一些推理模式,但代码问题经常产生简短、直接的响应,主要关注即时的代码输出,而初步分析或规划极少。

仅数学训练
仅使用数学数据进行训练,使得响应长度持续增加,并在数学基准测试中表现出色。重要的是,这培养了强大的、具有良好泛化能力的推理能力;当面对编码任务时,模型会尝试进行详细的逐步推理。观察到的行为包括在数学问题解决过程中进行细致的步骤检查和重新审视。这反映了数学数据激发推理能力的特性。

仅代码训练
尽管在代码基准测试上的表现有所提高,但显式推理行为的发展微乎其微,并且响应长度难以实现显著增加。与仅数学训练相比,对代码和数学问题的响应都明显更短,编码任务的解决方案通常是直接生成的,缺乏实质性的分步推理或初步分析。
分阶段训练
所提出的两阶段训练在数学和编码领域都展示了更优异的结果。该模型在解决数学问题时始终生成详细的逐步推理模式,以及用于编程任务的结构化推理模式。特别地,出现了复杂的行为,例如模型自发地利用代码生成作为辅助工具来协助数学推理。


历史重采样 (HR)
在训练期间,批次 (batches) 中有近 50% 的采样组会产生完全相同的奖励 (rewards)(见图8)。这种情况通常发生在模型持续成功解决较简单问题时,这导致奖励的方差极小,进而使得梯度更新 (gradient updates) 效率低下。
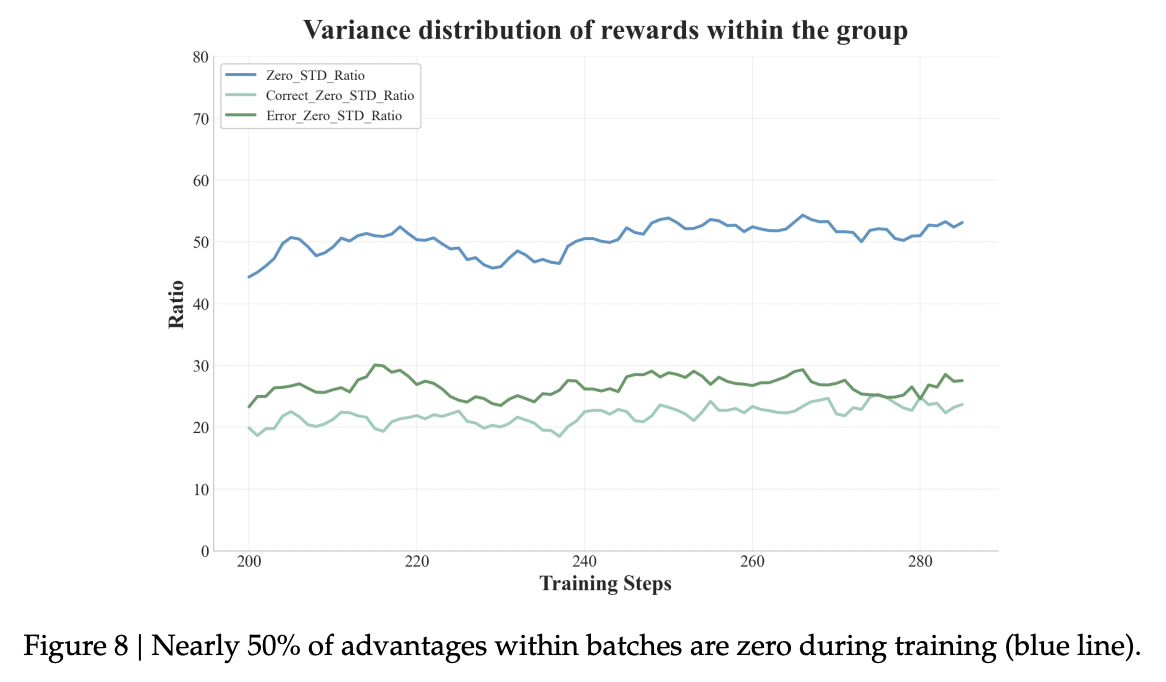
为了解决这种低效问题并提高梯度信号的质量,我们引入了历史重采样 (HR),一种轮次 (epoch) 级别的重采样机制。在训练过程中,我们记录每个轮次内所有推演 (rollout) 奖励的结果。在一个轮次结束时,我们按如下方式为下一个轮次重建数据集:
- 过滤掉“过于简单”的样本: 所有推演都得到正确答案的样本将被排除,因为它们无法为策略改进 (policy improvement) 提供有信息量的对比信号 (contrastive signals)。
- 保留“有信息量”的样本: 产生混合结果(既有正确推演也有错误推演)或完全是错误结果的样本将被保留。这些样本表现出正的奖励方差,确保了非零优势 (advantages) 和有效的梯度信号。此外,对于当前轮次内所有推演都错误的困难样本,我们也会将这些样本保留在数据集中。其逻辑在于,一些最初具有挑战性的问题对于更新后的策略可能会变得相对容易,从而在后续的推演中产生正优势。这种策略的基本思想与课程学习 (curriculum learning) 一致,即逐步让模型接触平均而言更具挑战性的样本,从而提高训练效率。
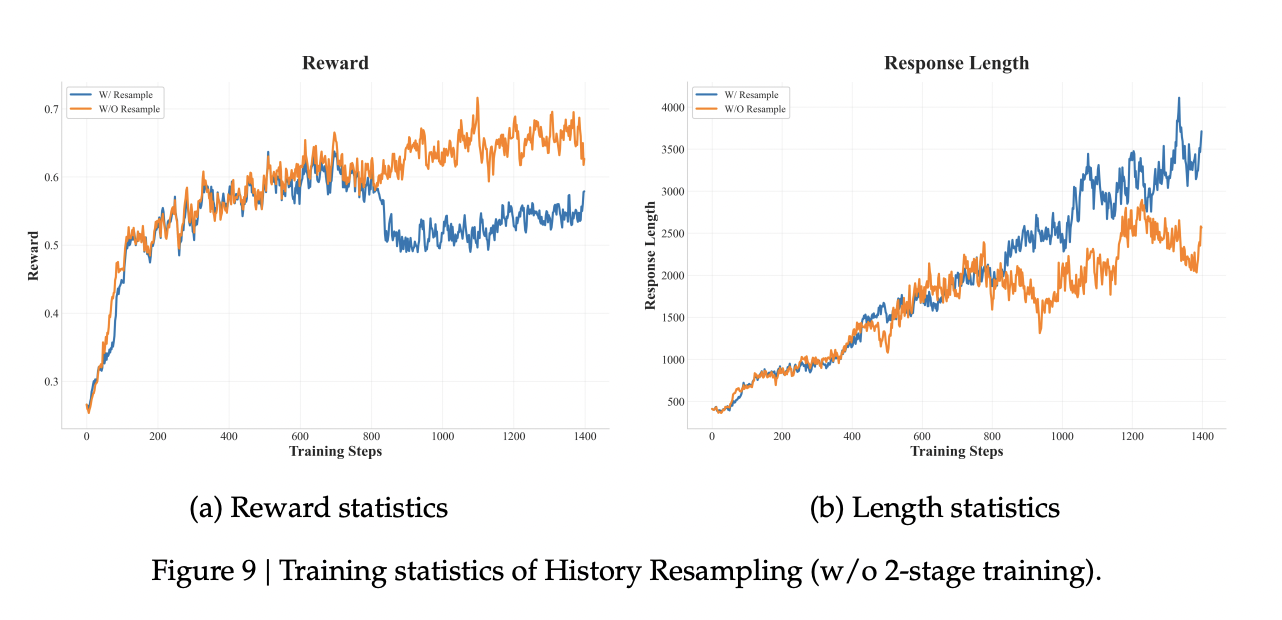
与动态调整推演次数的动态采样 (dynamic sampling) 方法相比,历史采样显著提高了计算效率。历史重采样对响应长度增长的积极影响如图9所示。
数据整理
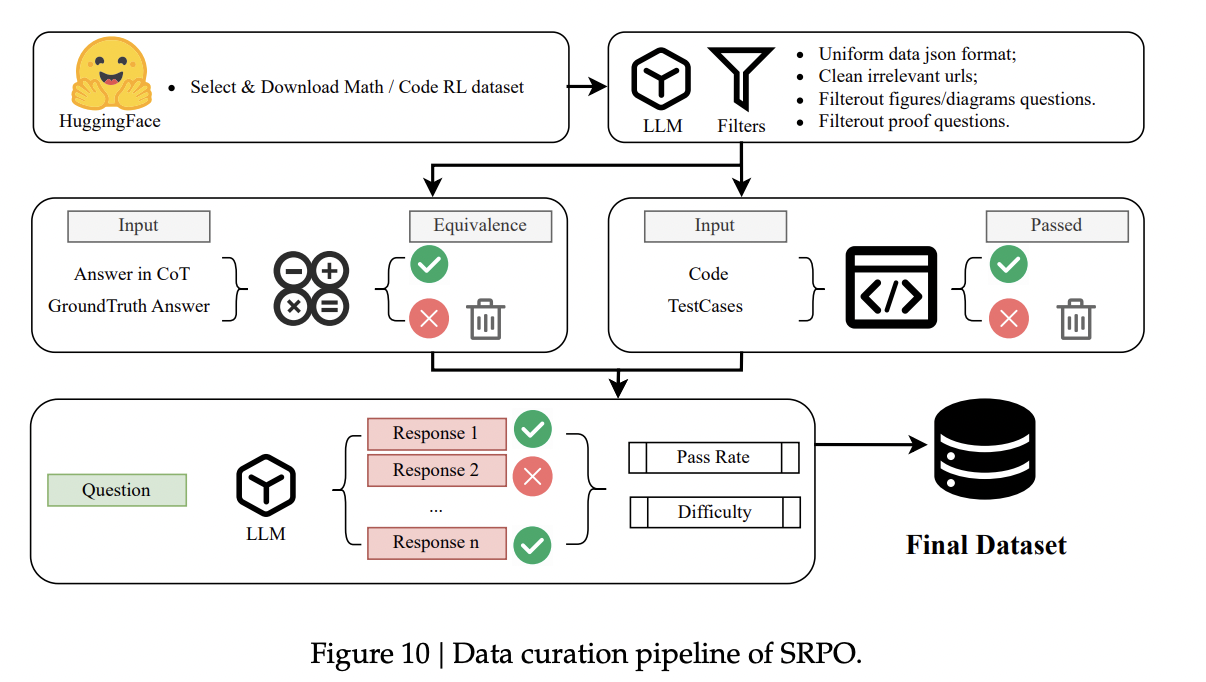
我们的数据整理流水线如图10所示。在下载阶段,我们从 HuggingFace 开源社区选择并下载与强化学习(RL)训练相关的数学和代码数据集。在清理阶段,数据集首先被转换为训练所需的 JSON 格式。样本中常见的无关 URL 会通过启发式方法进行清理。鉴于某些样本可能难以验证,甚至模型也无法解决,我们采用启发式规则和基于大语言模型(LLM)的方法来将其滤除。具体而言,对于数学样本,我们移除了那些包含多个问题、纯粹的证明题或需要图像/表格的样本。对于代码样本,我们排除了那些依赖特定环境或涉及文件 I/O 及网络交互的问题。
在验证阶段,我们确保数学问题和代码问题的正确性与清晰度。模型生成的解决方案是从其思维链(CoT)中提取的。代码解决方案在一组测试用例(最多 10 个)的沙盒环境中执行。数学解决方案则使用等价性验证器进行验证。未能通过此验证过程的样本将被过滤掉。此外,我们还评估答案的可理解性,剔除那些包含不正确解决方案或存在歧义的问题。最后,我们根据观察到的单次通过率(pass@1)和多次尝试成功率(pass@k),将经过验证的问题划分为三个难度级别:简单、中等和困难。
奖励设计
为了减轻由奖励模型引起的奖励操纵问题,我们采用了类似于 DeepSeek-R1 的基于规则的奖励系统设计,将最终奖励分为格式奖励和准确性奖励。对于格式奖励 $R_{format}$,我们要求模型的最终答案严格遵守“<output>答案</output>”的格式。遵守该格式得 0.2 分奖励;否则得 0 分。此外,模型响应中任何代码切换或混合多种语言的情况都将引入一个惩罚项:${Penalty}_{\text{mix}} = -0.1$。
$$ R_{\text{math}} = \begin{cases} 1, & \text{正确} \\ 0.2, & \text{部分正确} \\ 0, & \text{其他情况} \end{cases} $$$$ R_{\text{code}} = \begin{cases} 1, & \text{所有测试用例通过} \\ 0, & \text{其他情况} \end{cases} $$$$ R = R_{\text{math}/\text{code}} + R_{\text{format}} + {Penalty}_{\text{mix}} $$实验
在本节中,我们展示 SRPO 的详细实验结果。我们首先概述训练配置和关键超参数,阐明我们如何使用流行的优化技术。接下来,我们提供评估结果和设置。然后,我们考察训练动态,重点关注奖励趋势和响应长度等指标。最后,我们分析模型的思考行为。
训练设置
我们使用 Qwen-2.5-Base-32B 作为初始检查点,并采用 1e-6 的恒定学习率进行训练,使用 AdamW 优化器($\beta = [0.9, 0.95]$),不进行权重衰减。我们使用 vLLM 作为 rollout 推理框架,在每个步骤中采样 256 个提示词,每个提示词执行 32 次 rollout,小批量大小为 8,192,以进行严格的同策略强化学习(RL)训练。第一阶段训练进行 840 步,随后进入第二阶段。在每个 epoch 之后,我们执行历史重采样以移除过于简单的数据。
具体而言,我们应用 Token 级别的损失,并将超过最大响应长度(10,000 个 Token)的响应的优势值设置为零,以防止因长度偏差而进行裁剪。此外,考虑到推理模式与基础模型之间存在显著的分布差异,我们从 GRPO 损失函数中移除了 KL 项,以鼓励模型进行探索。
主要结果
我们的方法最终在 AIME 24 基准测试上取得了 50.0 pass@1 的成绩,在 LiveCodeBench(时间范围 2024-08 至 2025-01,版本与 DeepSeek 报告中所用相同)上取得了 41.6 pass@1 的成绩。这一表现超越了 DeepSeek-R1-Zero-Qwen-32B 的多领域 SOTA(State-of-the-Art)性能,并且在 AIME24 基准测试上达到了与当前最佳的基于 GRPO 的方法 DAPO 相当的水平。
| 模型 | AIME24 | LiveCodeBench |
|---|---|---|
| DeepSeek-R1-Zero-Qwen-32B | 47.0 | 40.2 |
| SRPO (本文方法) | 50.0 | 41.6 |
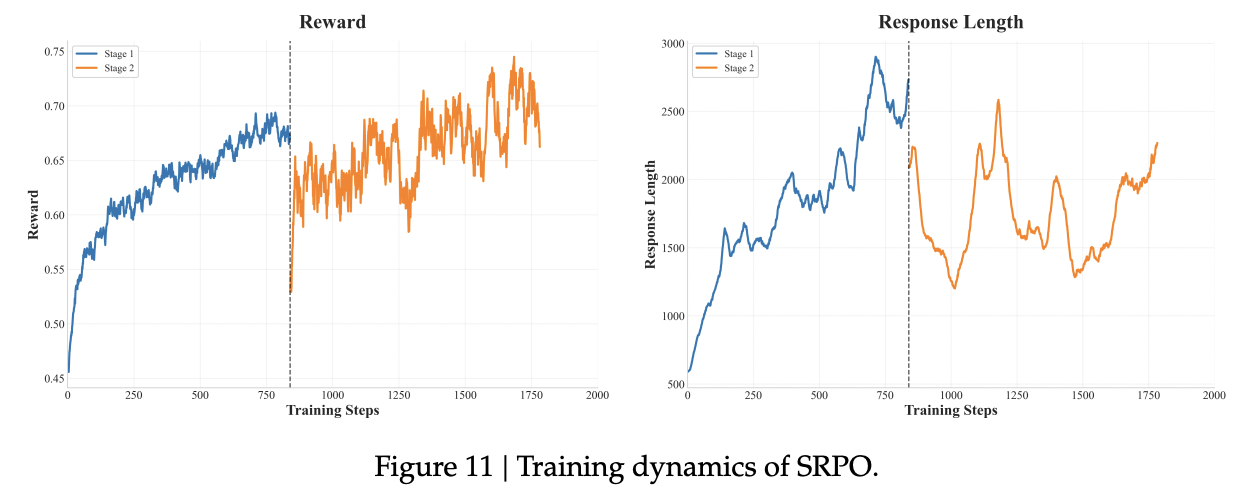
图11展示了 SRPO 训练的完整奖励曲线和响应长度曲线。我们在奖励增长开始趋于平稳后进入了第二阶段训练。在第二阶段开始时,由于模型先前未经训练的编码能力,整体奖励有所下降,随后的训练导致奖励稳步增加。在整合了编码数据后,响应长度并未显著增加,这与我们的预期一致,因为编码任务通常不需要更长的推理链。同时,基准测试结果表明模型的数学和编码能力均持续稳定提升,证明了我们方法的有效性。
特别地,所提出的历史重采样技术确保了在每个训练步骤中都能进行持续有效的梯度更新,直接增加了信息性梯度的比例。这种改进的样本效率带来了稳定的奖励增长,清楚地展示了我们的重采样策略所实现的训练效率提升。
思维行为分析
识别出三组代表性的反思模式。这些组包括复核(例如,“recheck”复查、“reevaluate”重新评估、“reexamine”复核、“rethink”反思、“double check”再次检查)、犹豫(“wait”等等、“but”但是、“maybe”也许、“aha”啊哈)和探索(“another way”另一种方式、“another approach”另一种途径、“another method”另一种方法、“but how”但是如何、“hold on”等一下)。我们将包含任何这些模式的响应数量计为“aha 响应”,并识别了平均响应长度(包括 aha 和非 aha 响应)。
我们惊讶地发现,在强化学习(RL)训练过程中,模型的自我反思、修正和回溯的频率逐渐增加。这表明模型展现了“自我验证”的能力。我们认为,这种类似于人类认知过程的“反思”的出现,代表了模型在强化学习中进行策略优化时表现出的一种适应性行为。
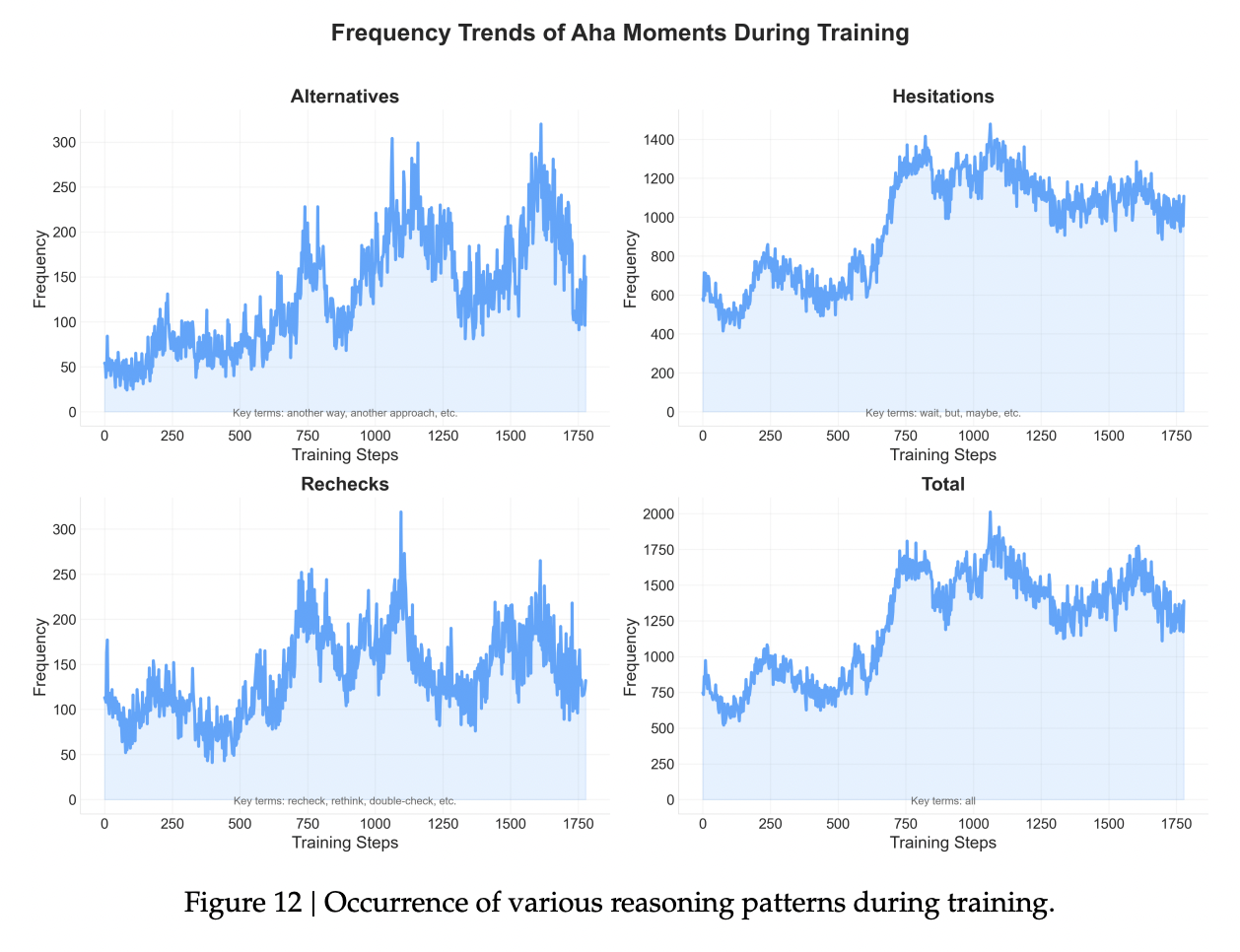
如图12所示,在模型训练的早期阶段,几乎没有检查和反思的证据。然而,随着训练的进行,模型表现出明显的反思和回溯行为,形成了诸如逐步推理、数值替换、逐一验证和自我优化等响应模式(案例见附录)。
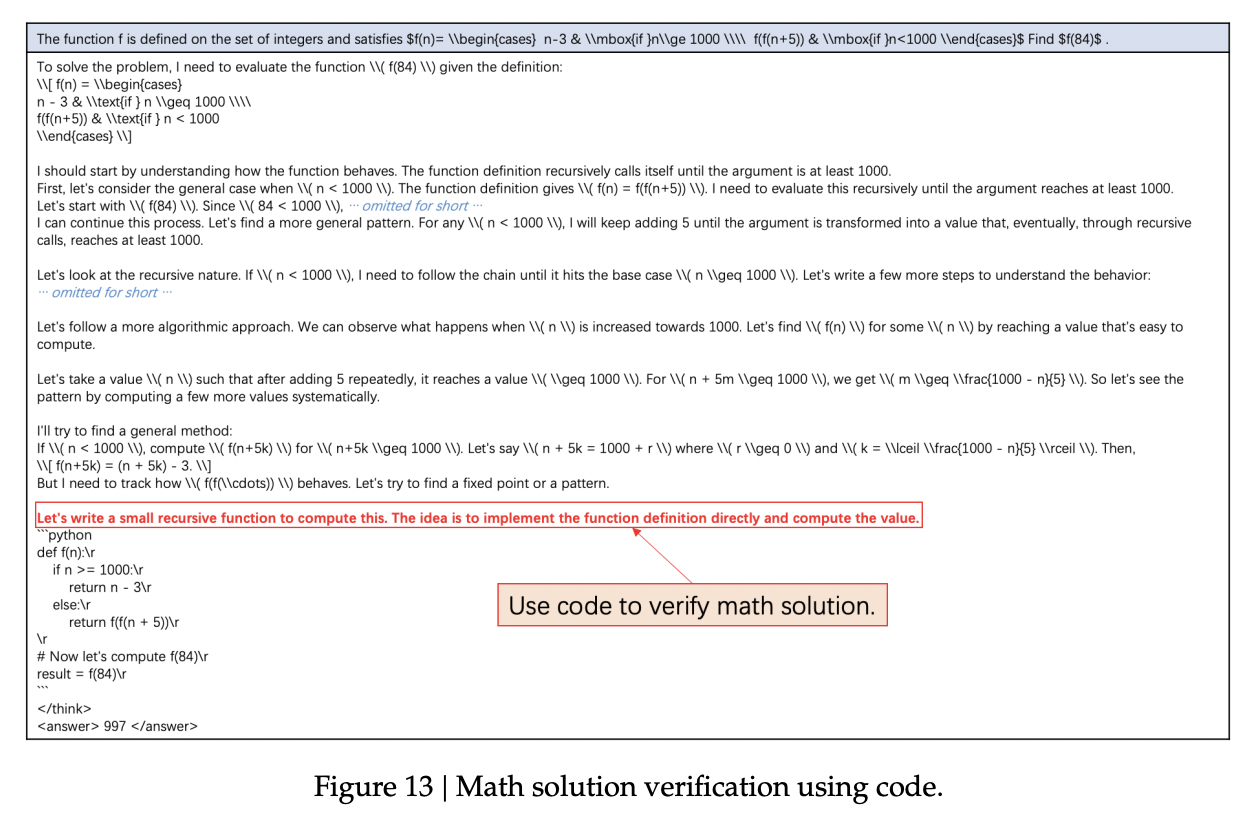
另一个有趣的观察是,在解决数学问题时会使用代码进行验证。例如,在上面的数学示例中(图13),模型首先通过数学推理给出解题过程,然后自发地编写程序代码来验证方案的结果。正如之前在两阶段训练部分所指出的,这类案例说明了模型如何运用程序性推理来自我纠正并进行后续尝试。此外,丰富的世界知识使得大语言模型(LLMs)能够以多种方式解决问题。结合使用多种方法成为一种自然的选择。这一现象进一步表明,模型已经掌握了在解决问题时进行广泛思考和使用广泛工具的技能。
结论
在本文中,我们介绍了两阶段历史重采样策略优化 (SRPO),这是首个在数学和代码任务上成功复现 DeepSeek-R1-Zero-Qwen-32B 推理性能的实现。我们提出了一个两阶段训练范式、epoch 级别的历史重采样方法,以及一个专为数学与代码联合强化学习训练量身定制的数据整理流程。我们详细的实验和实证见解为未来在可泛化的大规模强化学习研究领域提供了实践指导和宝贵的经验。
