摘要
Soft attention机制是驱动大语言模型 (LLM) 在给定上下文中定位相关部分的关键机制。然而,单个注意力权重仅由单个查询和键 Token 向量的相似性决定。这种“单 Token 注意力”限制了用于区分相关部分与上下文其余部分的信息量。为了解决这个问题,我们提出了一种新的注意力方法,多 Token 注意力(MTA),它允许大语言模型同时基于多个查询和键向量来调节其注意力权重。这是通过对查询、键和头应用卷积运算来实现的,从而允许附近的查询和键相互影响彼此的注意力权重,以实现更精确的注意力。因此,我们的方法可以使用更丰富、更细致的信息来定位相关上下文,这些信息可以超过单个向量的容量。通过广泛的评估,我们证明了 MTA 在一系列流行的基准测试中实现了增强的性能。值得注意的是,它在标准语言建模任务以及需要在长上下文中搜索信息的任务上优于 Transformer 基线模型,在这些任务中,我们的方法利用更丰富信息的能力被证明特别有益。
多头注意力机制背景
$$ K = H W_k , \quad V = H W_v, \quad Q = H W_q $$$$ \hat{A}={QK^\top}/{\sqrt{d}}, \quad A = \text{Softmax}( \text{Mask}_{-\infty}(\hat{A}) ), \label{eq:attn} $$其中 softmax 函数作用于 key 的维度,mask 函数将 $(i,j)$ 位置的值替换为 $-\infty$,当 $i
多Token注意力
$$ \begin{aligned} a_a = \text{Softmax}(q_a K^\top /{\sqrt{d}}), \quad \end{aligned} $$$$ a_r = \text{Softmax}(q_r K^\top /{\sqrt{d}}) $$通过使用这些查询进行常规的注意力机制,我们可以关注上下文中提到“Alice”和“rabbit”的位置。接下来,我们只需要检查注意力权重$a_a$和$a_r$是否在相同的附近位置(例如,在同一句话中)具有较高的概率,这将表明该句子同时提到了“Alice”和“rabbit”。不幸的是,常规的注意力机制缺乏注意力图之间的这种交互,而是仅使用它们来计算输出值。即使我们使用不同的注意力头来查找“Alice”和“rabbit”,也没有机制来组合这些注意力权重。这促使我们修改注意力机制,以允许组合来自附近位置(无论是查询还是键的位置),或者来自不同注意力头的不同注意力图。
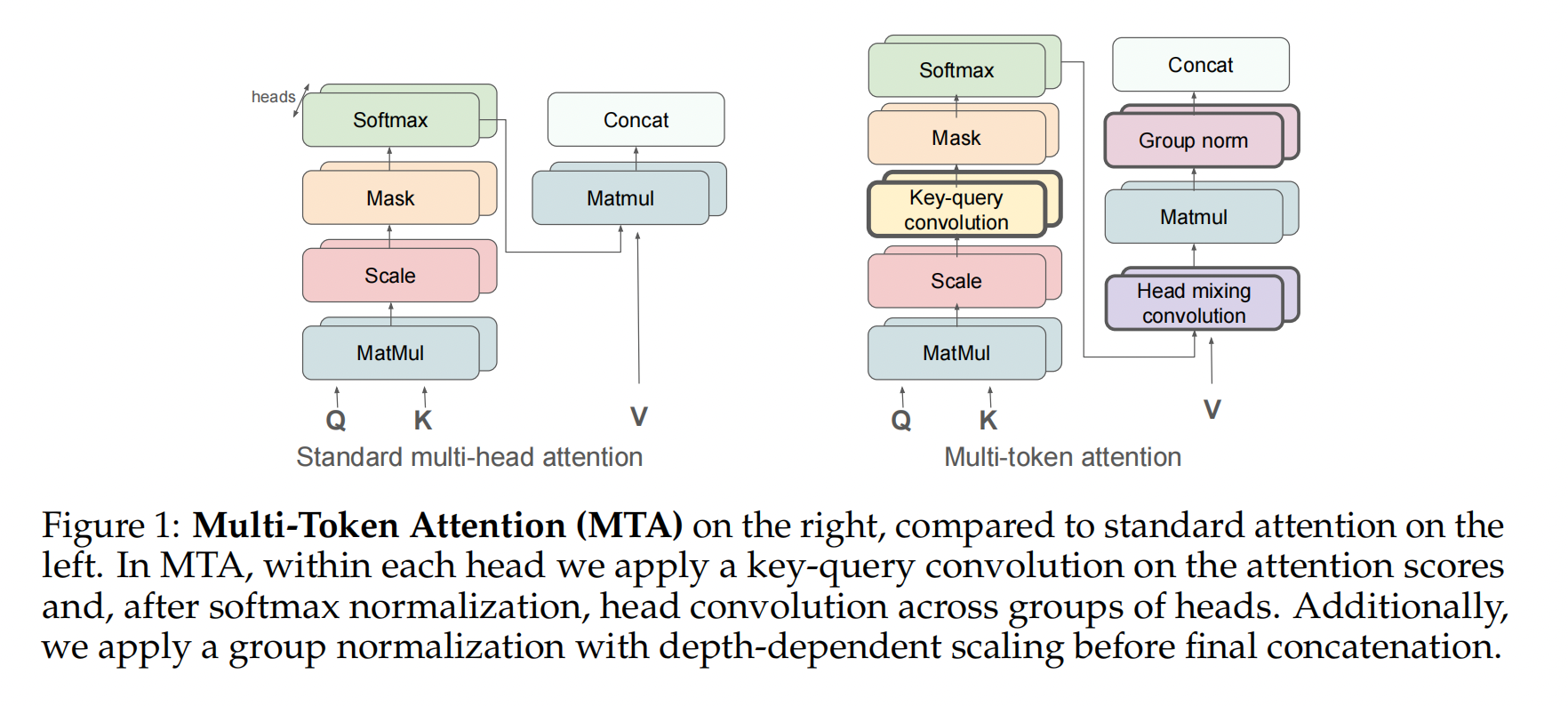
如图 1(右) 所示,我们提出的多 Token 注意力机制 (Multi-Token Attention) 包含三个重要的组成部分,它们构建在多头注意力机制之上:键-查询卷积、头混合卷积以及带有深度缩放的分组归一化。我们提出键-查询卷积来组合头内的多个键和查询,并提出头卷积来共享头之间的知识并放大重要信息。最后,我们应用带有深度缩放的分组归一化来对抗残差流并改善梯度流。在本节中,我们将描述 MTA 的工作原理。
Key-query convolution
Pre-softmax 卷积
$$ A = \text{Softmax}\left( \text{Conv2d}_\theta(\hat{A}) \right), $$其中 $\text{Conv2d}_\theta$ 是一个具有核权重 $\theta$ 和核大小 $(c_q, c_k)$ 的二维卷积操作。卷积应用于键和查询长度维度,而批次和头维度保持独立。更准确地说,从查询 $q_i$ 到键 $k_j$ 的注意力权重 $a_{ij}$ 计算如下:
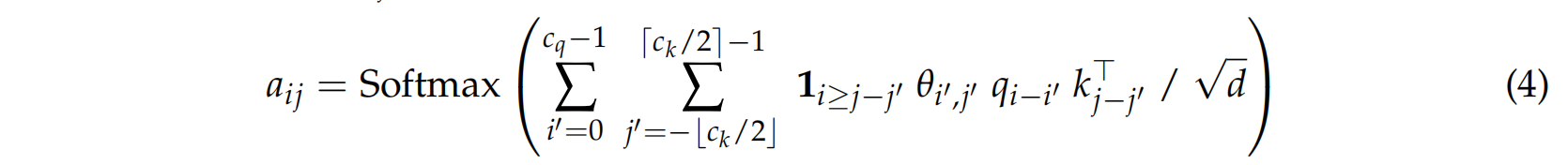
鉴于查询位置是 $i$,为了防止未来信息泄露,不应使用来自位置大于 $i$ 的任何信息。因此,公式中仅使用过去的查询。对于键,我们使用指示函数 $\mathbf{1}_{i \ge j-j'}$ 来屏蔽未来的键。然而,这种掩蔽实现起来过于复杂(需要修改卷积 CUDA 内核),因此我们提出了一个更简单的版本,它应用现有的因果掩蔽两次:
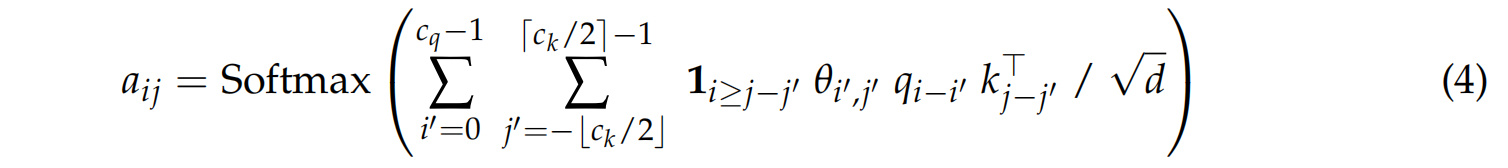
在这里,第一个掩码使用 0,目的是使这些值不影响卷积的输出。尽管这个版本屏蔽的内容略多于所需,但它更易于实现,并能防止信息泄露,因此我们将其作为默认设置使用。
Post-softmax 卷积
$$ A = \text{Mask}_0\left( \text{Conv2d}_\theta \left( \text{Softmax}\left( \text{Mask}_{-\infty}( \hat{A}) \right) \right) \right) . $$这使得注意力权重之间的交互是加性的,而不是乘性的。我们将尝试这两种版本,但默认情况下将使用 pre-softmax 版本。
每个注意力头都有单独的 $\theta$ 参数,因此它们可以执行不同的卷积操作。选择的内核维度决定了 Token 可以组合在一起的距离。在上面的例子中,问题“Alice 在哪里看到兔子?”将使 $q_a$ 和 $q_r$ 查询被两个 Token 分隔(假设使用单词 Tokenizer),因此我们需要 $c_q=4$ 来覆盖这两个查询。类似地,目标句子“Alice saw the white rabbit under the tree”例如产生被三个 Token 分隔的键 $k_a$ 和 $k_r$,因此 $c_k=5$ 足以将它们组合起来。在应用卷积之前,我们用适当数量的零填充输入,以便每个卷积操作都有一个有效的输入。
头部混合卷积
$$ \label{eq:head_mix} A_\text{new}^1 = w_{11} A^1 + w_{12} A^2 ,\\ \quad A_\text{new}^2 = w_{21} A^1 + w_{22} A^2 , $$$$ \begin{aligned} \hat{A}_\text{new}^1 = w_{11} \hat{A}^1 + w_{12} \hat{A}^2 ,\\ \quad \hat{A}_\text{new}^2 = w_{21} \hat{A}^1 + w_{22} \hat{A}^2 , \end{aligned} $$与键-查询卷积一样,我们对这两个版本都进行了实验。
整合所有内容
在前几节中,我们介绍了两种不同的混合注意力权重的方法,一种是在键-查询时间步长上混合,另一种是在不同的头之间混合。这两种方法可以在一个单一的 MTA 模块中一起实现。因为每种方法都有 softmax 前和 softmax 后的版本,所以有多种不同的组合方式。
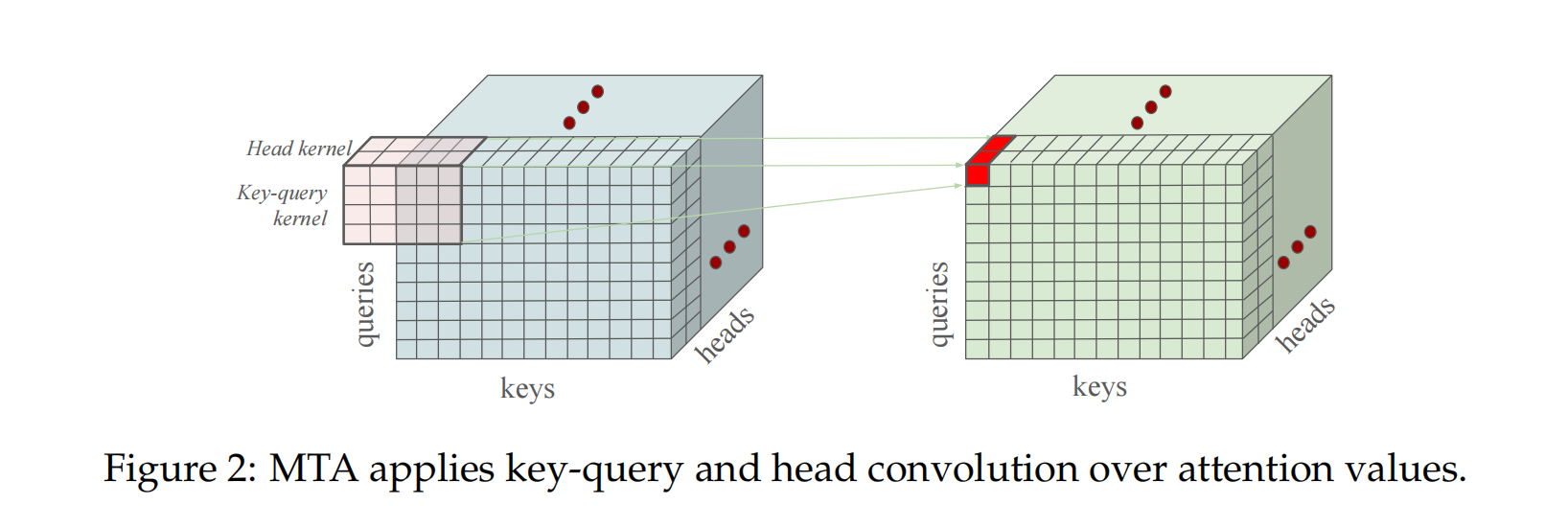
如果两种混合方法都是 softmax 前的,那么它们可以通过一个单一的 3 维卷积操作来实现,如图2所示。其中两个维度将跨越键和查询维度。第三个维度将跨越注意力头,但在 $c_h$ 个头的组上。同样的 3 维卷积也可以在 softmax 后应用,以执行两种混合方法的 softmax 后版本。
第三种可能性是在 softmax 前应用键-查询卷积,然后在 softmax 后进行头混合。
最后,我们遵循 @ye2024differential 的方法,对每个头独立应用具有层相关缩放的归一化,以改善梯度流动。我们还报告了没有这一步骤的结果。
实验
我们采用 MTA 架构进行实验,并在一系列标准和长程依赖任务上,将其与多个基线模型进行比较,首先从一个玩具任务开始。除非另有说明,否则我们在 softmax 之前应用键-查询卷积,并在 softmax 之后应用头混合。
大语言模型建模
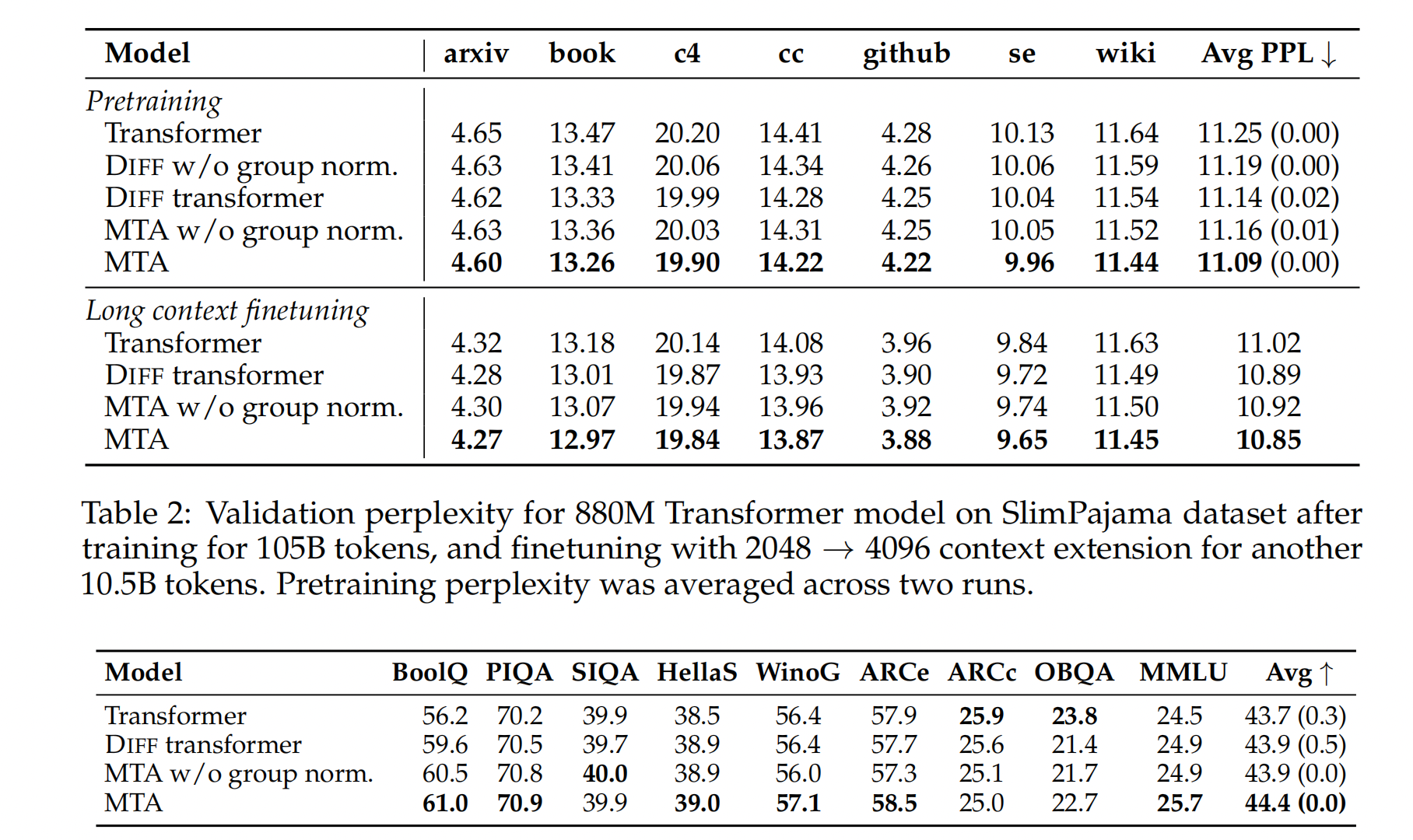
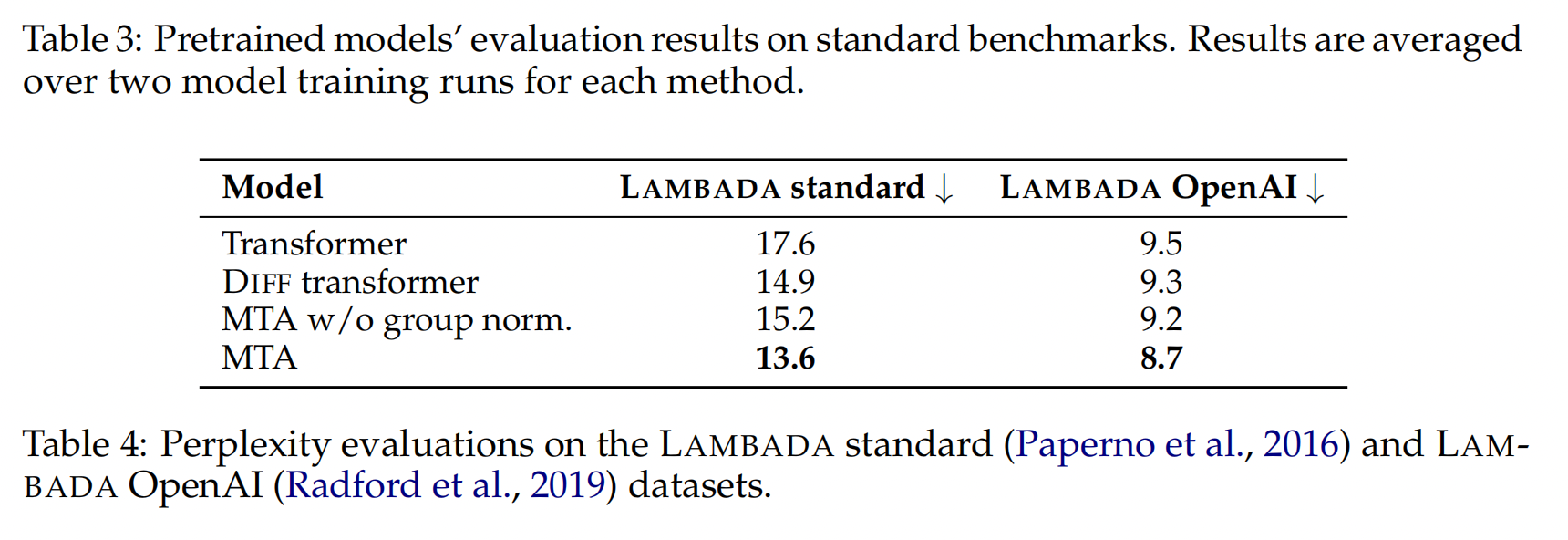
长文本上下文微调|长程依赖任务
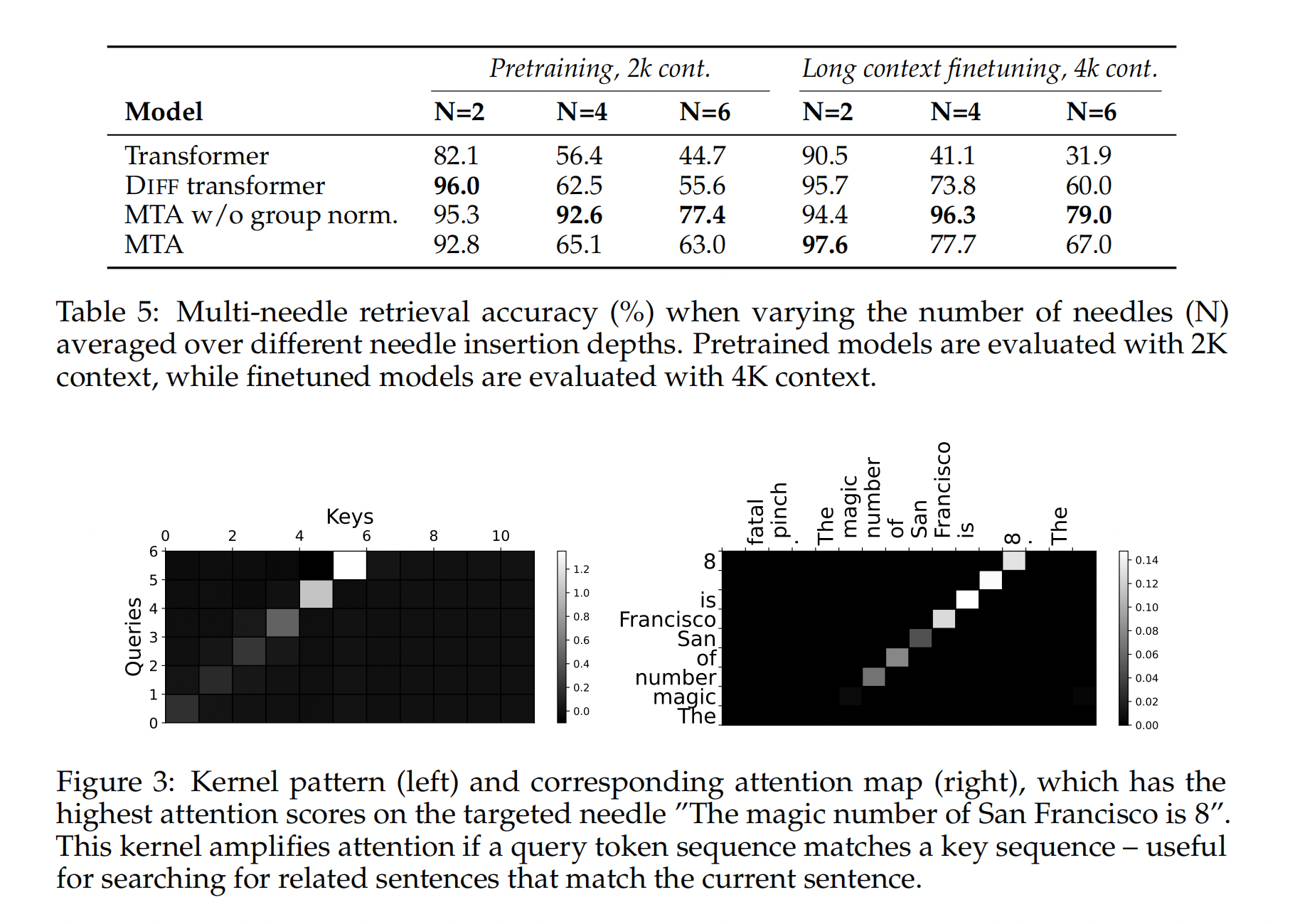
核模式
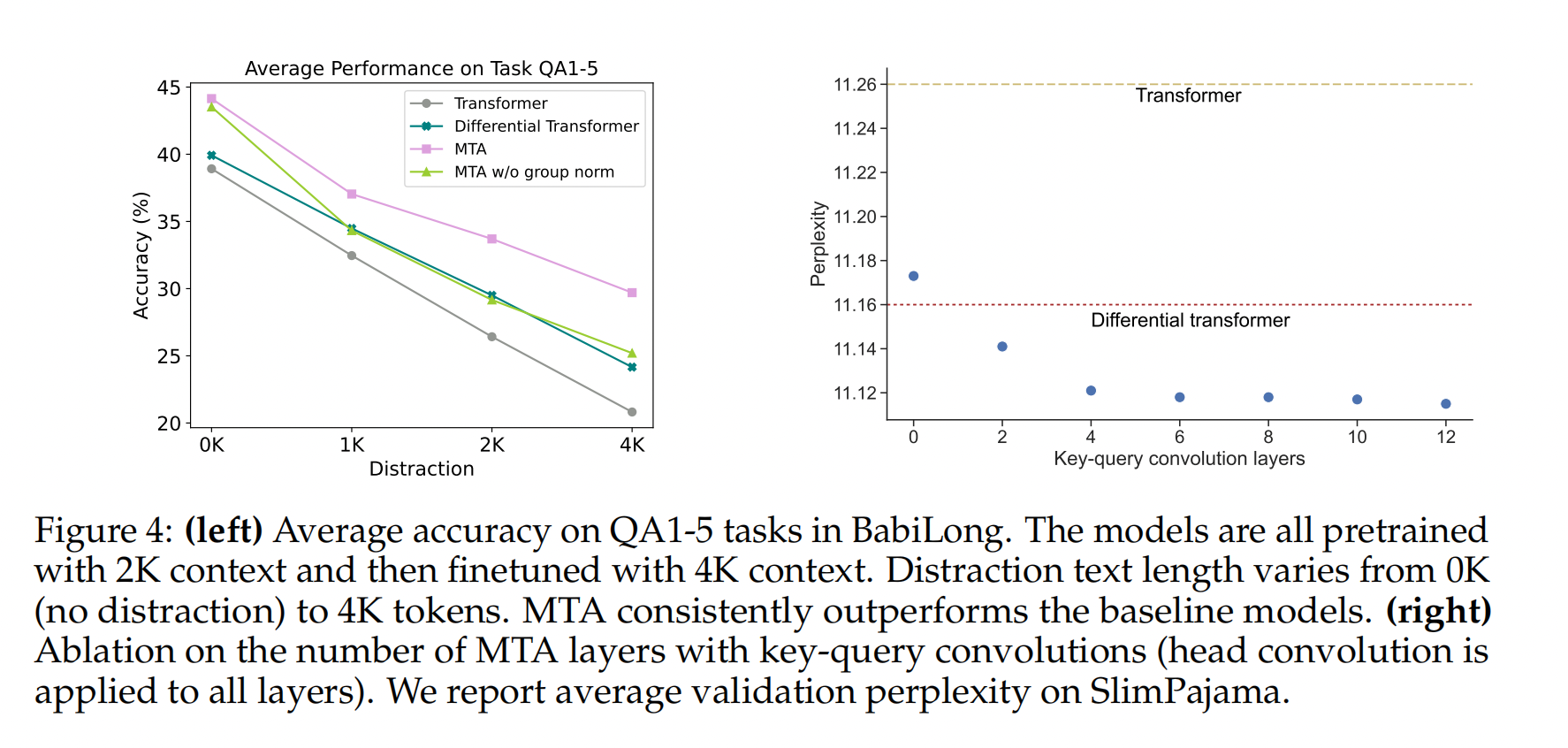
MTA 组件的消融实验